Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T17:09:51.848Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximating gamma distributions by normalized negative binomial distributions

Part of: Integral transforms, operational calculus Special processes Approximations and expansions Distribution theory Limit theorems

Published online by Cambridge University Press:  14 July 2016

José A. Adell  and
Jesús De La Cal
José A. Adell*
Affiliation:
Universidad de Zaragoza
Jesús De La Cal*
Affiliation:
Universidad del País Vasco
*
∗ Postal address: Departamento de Métodos Estadísticos, Facultad de Ciencias, Universidad de Zaragoza, E-50009 Zaragoza, Spain.
∗∗ Postal address: Departamento de Matemática Aplicada y Estadística e Investigación Operativa, Facultad de Ciencias, Universidad del País Vasco, Apartado 644, E-48080 Bilbao, Spain.
Get access Rights & Permissions [Opens in a new window]

Abstract

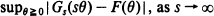Let F be the gamma distribution function with parameters a > 0 and α > 0 and let Gs be the negative binomial distribution function with parameters α and a/s, s > 0. By combining both probabilistic and approximation-theoretic methods, we obtain sharp upper and lower bounds for . In particular, we show that the exact order of uniform convergence is s–p, where p = min(1, α). Various kinds of applications concerning charged multiplicity distributions, the Yule birth process and Bernstein-type operators are also given.

Keywords

UNIFORM DISTANCERATE OF CONVERGENCECHARGED MULTIPLICITY DISTRIBUTIONSBASKAKOV OPERATORGAMMA OPERATOR

MSC classification

Primary: 62E20: Asymptotic distribution theory 60F05: Central limit and other weak theorems
Secondary: 44A10: Laplace transform 41A99: None of the above, but in this section 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Type
Research Papers
Information
Journal of Applied Probability , Volume 31 , Issue 2 , June 1994 , pp. 391 - 400
Copyright
Copyright © Applied Probability Trust 1994 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported by CAI-CONAI PCB0292 and by the University of the Basque Country.

References

Adell, J. A. and De La Cal, J. (1993) On the uniform convergence of normalized Poisson mixtures to their mixing distribution. Statist. Prob. Lett. 18, 227–232.Google Scholar
Adell, J. A. and De La Cal, J. (1993) On a Bernstein-type operator associated with the inverse Pólya-Eggenberger distribution. Rend. Circ. Mat. Palermo. To appear.Google Scholar
Alner, G. J. et al. (Ua5 Collaboration) (1985a) Multiplicity distributions in different pseudorapidity intervals at a CMS energy of 540 GeV. Phys. Lett. B 160, 193–198.Google Scholar
Alner, G. J. et al. (Ua5 Collaboration) (1985b) A new empirical regularity for multiplicity distributions in place of KNO scaling. Phys. Lett B 160, 199–206.Google Scholar
Barbour, A. D. and Hall, P. (1984) On the rate of Poisson convergence. Math. Proc. Camb. Phil. Soc. 95, 473–480.Google Scholar
Carruthers, P. and Shih, C. C. (1987) The phenomenological analysis of hadronic multiplicity distributions. Internat. J. Modern Phys. A 2, 1447–1547.Google Scholar
De La Cal, J. and Luquin, F. (1992) A note on limiting properties of some Bernstein-type operators. J. Approx. Theory 68, 322–329.Google Scholar
De La Cal, J. and Luquin, F. (1994) Approximating Szász and Gamma operators by Baskakov operators. J. Math. Anal. Appl. To appear.Google Scholar
De Vore, R. (1972) The Approximation of Continuous Functions by Positive Linear Operators. Lecture Notes in Mathematics, Vol. 293, Springer-Verlag, New York.CrossRefGoogle Scholar
Feller, W. (1966) An Introduction to Probability Theory and Its Applications, Vol. II. Wiley, New York.Google Scholar
Giacomelli, G. (1990) Inclusive and semi-inclusive hadron interactions at ISR and collider energies. Internat J. Modern Phys. A 5, 223–297.Google Scholar
Gregoire, G. (1983) Negative binomial distributions for point processes. Stoch. Proc. Appl. 16, 179–188.CrossRefGoogle Scholar
Johnson, N. L. and Kotz, S. (1969) Discrete Distributions. Houghton-Mifflin, Boston.Google Scholar
Johnson, N. L. and Kotz, S. (1970) Continuous Univariate Distributions-1. Wiley, New York.Google Scholar
Karlin, S. and Taylor, H. M. (1975) A First Course in Stochastic Processes, 2nd edn. Academic Press, New York.Google Scholar
Lindsay, G. (1989) Moment matrices: applications in mixtures. Ann. Statist. 17, 722–740.Google Scholar
Petrov, V. V. (1975) Sums of Independent Random Variables. Springer, New York.Google Scholar
Pfeifer, D. (1987) On the distance between mixed Poisson and Poisson distributions. Statist. Decisions 5, 367–379.Google Scholar
Vervaat, W. (1969) Upper bounds for the distance in total variation between the binomial or negative binomial and the Poisson distribution. Statist. Neerlandica 23, 79–86.Google Scholar