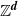Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T16:56:23.509Z Has data issue: false hasContentIssue false
  • English
  • Français

An invariance principle and a large deviation principle for the biased random walk on ${\mathbb{Z}}^{\lowercase{\textbf{\textit{d}}}}$

Part of: Graph theory Limit theorems Markov processes

Published online by Cambridge University Press:  04 May 2020

Yuelin Liu ,
Vladas Sidoravicius ,
Longmin Wang  and
Kainan Xiang
Yuelin Liu*
Affiliation:
Nankai University
Vladas Sidoravicius*
Affiliation:
CIMS; NYU-Shanghai
Longmin Wang*
Affiliation:
Nankai University
Kainan Xiang*
Affiliation:
Xiangtan University
*
*Postal address: School of Mathematical Sciences, LPMC, Nankai University, Tianjin, 300071, China.
***Postal address: Courant Institute of Mathematical Sciences, New York, NY10012, USA; NYU-ECNU Institute of Mathematical Sciences, NYU-Shanghai, Shanghai, 200122, China.
*Postal address: School of Mathematical Sciences, LPMC, Nankai University, Tianjin, 300071, China.
****Postal address: School of Mathematics and Computational Science, Xiangtan University, Xiangtan City, 411105, China.
Get access Rights & Permissions [Opens in a new window]

Abstract

We establish an invariance principle and a large deviation principle for a biased random walk 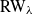${\text{RW}}_\lambda$ with 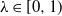$\lambda\in [0,1)$ on 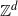$\mathbb{Z}^d$ . The scaling limit in the invariance principle is not a d-dimensional Brownian motion. For the large deviation principle, its rate function is different from that of a drifted random walk, as may be expected, though the reflected biased random walk evolves like the drifted random walk in the interior of the first quadrant and almost surely visits coordinate planes finitely many times.

Keywords

Biased random walkinvariance principlelarge deviation principle

MSC classification

Primary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces) 05C81: Random walks on graphs
Secondary: 60F05: Central limit and other weak theorems 60F10: Large deviations
Type
Research Papers
Information
Journal of Applied Probability , Volume 57 , Issue 1 , March 2020 , pp. 295 - 313
Copyright
© Applied Probability Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aϊdékon, E. (2014). Speed of the biased random walk on a Galton–Watson tree. Prob. Theory Relat. Fields 159, 597–617.CrossRefGoogle Scholar
Arous, G. B. and Fribergh, A. (2016). Biased random walks on random graphs. In Probability and Statistical Physics in St. Petersburg, eds V. Sidoravicius and S. Smirnov, 91, 99–153.Google Scholar
Arous, G. B., Fribergh, A., Gantert, N. and Hammond, A. (2015) Biased random walks on Galton–Watson trees with leaves. Ann. Prob. 40, 280–338.CrossRefGoogle Scholar
Arous, G. B., Hu, Y. Y., Olla, S. and Zeitouni, O. (2013). Einstein relation for biased random walk on Galton–Watson trees. Ann. Inst. H. Poincaré Prob. Statist. 49, 698–721.CrossRefGoogle Scholar
Berretti, A. and Sokal, A. D. (1985). New Monte Carlo method for the self-avoiding walk. J. Stat. Phys. 40, 483–531.CrossRefGoogle Scholar
Bowditch, A. (2018). A quenched central limit theorem for biased random walks on supercritical Galton–Watson trees. J. Appl. Prob. 55, 610–626.CrossRefGoogle Scholar
Dembo, A. and Zeitouni, O. (1998). Large Deviations Techniques and Applications, 2nd edn. Springer, New York.CrossRefGoogle Scholar
Durrett, R. (2010). Probability Theory and Examples, 4th edn. Cambridge University Press.CrossRefGoogle Scholar
Ethier, E. N. and Kurtz, T. G. (2005). Markov Processes: Characterization and Convergence. John Wiley, New York.Google Scholar
Hu, Y. Y. and Shi, Z. (2015). The most visited sites of biased random walks on trees. Electron. J. Prob. 20, 1–14.CrossRefGoogle Scholar
Jones, G. L. (2004). On the Markov chain central limit theorem. Prob. Surv. 1, 299–320.CrossRefGoogle Scholar
Lawler, G. F. and Sokal, A. D. (1988). Bounds on the $L^2$ spectrum for Markov chains and Markov processes: a generalization of Cheeger’s inequality. Trans. Amer. Math. Soc. 309, 557–580.Google Scholar
Lyons, R. (1990). Random walks and percolation on trees. Ann. Prob. 18, 931–958.CrossRefGoogle Scholar
Lyons, R. (1992). Random walks, capacity, and percolation on trees. Ann. Prob. 20, 2043–2088.CrossRefGoogle Scholar
Lyons, R. (1995). Random walks and the growth of groups. C. R. Acad. Sci. Paris 320, 1361–1366.Google Scholar
Lyons, R., Pemantle, R. and Peres, Y. (1996). Biased random walks on Galton–Watson trees. Prob. Theory Relat. Fields 106, 249–264.CrossRefGoogle Scholar
Lyons, R., Pemantle, R. and Peres, Y. (1996). Random walks on the lamplighter group. Ann. Prob. 24, 1993–2006.Google Scholar
Lyons, R. and Peres, Y. (2016). Probability on Trees and Networks. Cambridge University Press.CrossRefGoogle Scholar
Merlevède, F., Peligrad, M. and Utev, S. (2006). Recent advances in invariance principles for stationary sequences. Prob. Surv. 3, 1–36.CrossRefGoogle Scholar
Randall, D. (1994). Counting in lattices: combinatorial problems for statistical mechanics. PhD thesis, University of California.Google Scholar
Shi, Z., Sidoravicius, V., Song, H., Wang, L. and Xiang, K. (2018). Uniform spanning forests associated with biased random walks on Euclidean lattices. Preprint. Available at http://arxiv.org/abs/1805/01615v1 .Google Scholar
Sinclair, A. J. and Jerrum, M. R. (1989). Approximate counting, uniform generation and rapidly mixing Markov chains. Inf. Comput. 82, 93–133.CrossRefGoogle Scholar