Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chan, Terence
and
Jansons, Kalvis M.
1997.
Semiflexible polymers in straining flows.
Journal of Statistical Physics,
Vol. 88,
Issue. 1-2,
p.
145.
Manton, Kenneth G.
and
Yashin, Anatoli I.
1997.
Effects of unobserved and partially observed covariate processes on system failure: a review of models and estimation strategies.
Statistical Science,
Vol. 12,
Issue. 1,
Ebrahimi, Nader
2001.
A stochastic covariate failure model for assessing system reliability.
Journal of Applied Probability,
Vol. 38,
Issue. 3,
p.
761.
Ebrahimi, Nader
2001.
A stochastic covariate failure model for assessing system reliability.
Journal of Applied Probability,
Vol. 38,
Issue. 03,
p.
761.
Kleptsyna, M.L.
and
Le Breton, A.
2002.
A Cameron-Martin type formula for general Gaussian processes--a filtering approach.
Stochastics and Stochastic Reports,
Vol. 72,
Issue. 3-4,
p.
229.
Deheuvels, Paul
Peccati, Giovanni
and
Yor, Marc
2006.
On quadratic functionals of the Brownian sheet and related processes.
Stochastic Processes and their Applications,
Vol. 116,
Issue. 3,
p.
493.
Марихин, Владимир Георгиевич
Marikhin, Vladimir Georgievich
Соколов, Владимир Вячеславович
and
Sokolov, Vladimir Vyacheslavovich
2010.
О некоторых интегральных уравнениях, связанных со случайными гауссовскими процессами.
Теоретическая и математическая физика,
Vol. 164,
Issue. 2,
p.
196.
Marikhin, V. G.
and
Sokolov, V. V.
2010.
Some integral equations related to random Gaussian processes.
Theoretical and Mathematical Physics,
Vol. 164,
Issue. 2,
p.
992.
Lototsky, S.V.
and
Moers, M.
2015.
Large-time and small-ball asymptotics for quadratic functionals of Gaussian diffusions.
Asymptotic Analysis,
Vol. 95,
Issue. 3-4,
p.
345.
Arbeev, Konstantin G.
Cohen, Alan A.
Arbeeva, Liubov S.
Milot, Emmanuel
Stallard, Eric
Kulminski, Alexander M.
Akushevich, Igor
Ukraintseva, Svetlana V.
Christensen, Kaare
and
Yashin, Anatoliy I.
2016.
Optimal Versus Realized Trajectories of Physiological Dysregulation in Aging and Their Relation to Sex-Specific Mortality Risk.
Frontiers in Public Health,
Vol. 4,
Issue. ,


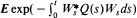 where
where 