Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-29T08:16:22.240Z Has data issue: false hasContentIssue false
  • English
  • Français

An adjacent-swap Markov chain on coalescent trees

Part of: Markov processes

Published online by Cambridge University Press:  02 September 2022

Mackenzie Simper Open the ORCID record for Mackenzie Simper [Opens in a new window]  and
Julia A. Palacios
Mackenzie Simper*
Affiliation:
Stanford University
Julia A. Palacios*
Affiliation:
Stanford University
*
*Postal address: Department of Mathematics, Building 380, 450 Jane Stanford Way, Stanford, CA 94305, USA. Email address: [email protected]
**Postal address: Department of Statistics and Department of Biomedical Data Science, Sequoia Hall, 390 Jane Stanford Way, Stanford, CA 94305, USA. Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The standard coalescent is widely used in evolutionary biology and population genetics to model the ancestral history of a sample of molecular sequences as a rooted and ranked binary tree. In this paper we present a representation of the space of ranked trees as a space of constrained ordered matched pairs. We use this representation to define ergodic Markov chains on labeled and unlabeled ranked tree shapes analogously to transposition chains on the space of permutations. We show that an adjacent-swap chain on labeled and unlabeled ranked tree shapes has a mixing time at least of ord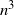er $n^3$ , and at most of order 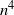$n^{4}$ . Bayesian inference methods rely on Markov chain Monte Carlo methods on the space of trees. Thus it is important to define good Markov chains which are easy to simulate and for which rates of convergence can be studied.

Keywords

Random transpositionslumped Markov chainTajima distribution

MSC classification

Primary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Type
Original Article
Information
Journal of Applied Probability , Volume 59 , Issue 4 , December 2022 , pp. 1243 - 1260
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aldous, D. (1983). Random walks on finite groups and rapidly mixing Markov chains. In Séminaire de Probabilités XVII 1981/82, pp. 243–297. Springer.CrossRefGoogle Scholar
Aldous, D. J. (2000). Mixing time for a Markov chain on cladograms. Combinatorics Prob. Comput. 9, 191–204.Google Scholar
Cappello, L. and Palacios, J. A. (2020). Sequential importance sampling for multiresolution Kingman–Tajima coalescent counting. Ann. Appl. Statist. 14, 727–751.CrossRefGoogle ScholarPubMed
Cappello, L., Veber, A. and Palacios, J. A. (2020). The Tajima heterochronous n-coalescent: Inference from heterochronously sampled molecular data. Available at arXiv:2004.06826.Google Scholar
Diaconis, P. W. and Holmes, S. P. (1998). Matchings and phylogenetic trees. Proc. Nat. Acad. Sci. USA 95, 14600–14602.CrossRefGoogle Scholar
Diaconis, P. and Holmes, S. (2002). Random walks on trees and matchings. Electron. J. Prob. 7, 1–17.CrossRefGoogle Scholar
Diaconis, P. and Wood, P. M. (2013). Random doubly stochastic tridiagonal matrices. Random Structures Algorithms 42, 403–437.CrossRefGoogle Scholar
Dinh, V., Darling, A. E. and Matsen, IV, F. A. (2018). Online Bayesian phylogenetic inference: Theoretical foundations via sequential Monte Carlo. Syst. Biol. 67, 503–517.CrossRefGoogle ScholarPubMed
Donaghey, R. (1975). Alternating permutations and binary increasing trees. J. Combinatorial Theory A 18, 141–148.CrossRefGoogle Scholar
Drummond, A., Suchard, M., Xie, D. and Rambaut, A. (2012). Bayesian phylogenetics with BEAUti and the BEAST 1.7. Mol. Biol. Evol. 29, 1969–1973.CrossRefGoogle ScholarPubMed
Durrett, R. (2003). Shuffling chromosomes. J. Theoret. Prob. 16, 725–750.Google Scholar
Felsenstein, J. (2004). Inferring Phylogenies, Vol. 2. Sinauer Associates, Sunderland, MA.Google Scholar
Friedman, N., Ninio, M., Pe’er, I. and Pupko, T. (2001). A structural EM algorithm for phylogenetic inference. In Proceedings of the Fifth Annual International Conference on Computational Biology, pp. 132–140.CrossRefGoogle Scholar
Frost, S. D. W. and Volz, E. M. (2013). Modelling tree shape and structure in viral phylodynamics. Phil. Trans. R. Soc. B 368, 20120208.CrossRefGoogle ScholarPubMed
Janson, S. and Kersting, G. (2011). On the total external length of the Kingman coalescent. Electron. J. Prob. 16, 2203–2218.CrossRefGoogle Scholar
Kingman, J. (1982). The coalescent. Stoch. Process. Appl. 13, 235–248.CrossRefGoogle Scholar
Kirkpatrick, M. and Slatkin, M. (1993). Searching for evolutionary patterns in the shape of a phylogenetic tree. Evolution 47, 1171–1181.CrossRefGoogle Scholar
Kuznetsov, A. G., Pak, I. M. and Postnikov, A. E. (1994). Increasing trees and alternating permutations. Russian Math. Surveys 49, 79.CrossRefGoogle Scholar
Lacoin, H. (2016). Mixing time and cutoff for the adjacent transposition shuffle and the simple exclusion. Ann. Prob. 44, 1426–1487.CrossRefGoogle Scholar
Levin, D. A. and Peres, Y. (2017). Markov Chains and Mixing Times, American Mathematical Society.CrossRefGoogle Scholar
Liu, S., Westbury, M. V., Dussex, N., Mitchell, K. J., Sinding, M.-H. S., Heintzman, P. D., Duchêne, D. A., Kapp, J. D., von Seth, J., Heiniger, H. et al. (2021). Ancient and modern genomes unravel the evolutionary history of the rhinoceros family. Cell 184, 4874–4885.CrossRefGoogle ScholarPubMed
Maliet, O., Gascuel, F. and Lambert, A. (2018). Ranked tree shapes, nonrandom extinctions, and the loss of phylogenetic diversity. Syst. Biol. 67, 1025–1040.CrossRefGoogle ScholarPubMed
Misra, N., Blelloch, G., Ravi, R. and Schwartz, R. (2011). An optimization-based sampling scheme for phylogenetic trees. In International Conference on Research in Computational Molecular Biology (Lecture Notes in Computer Science 6577), pp. 252–266. Springer, Berlin and Heidelberg.CrossRefGoogle Scholar
Mossel, E. and Vigoda, E. (2006). Limitations of Markov chain Monte Carlo algorithms for Bayesian inference of phylogeny. Ann. Appl. Prob. 16, 2215–2234.Google Scholar
Palacios, J. A., Véber, A., Cappello, L., Wang, Z., Wakeley, J. and Ramachandran, S. (2019). Bayesian estimation of population size changes by sampling Tajima’s trees. Genetics 213, 967–986.CrossRefGoogle ScholarPubMed
Rajanala, S. and Palacios, J. A. (2021). Statistical summaries of unlabelled evolutionary trees and ranked hierarchical clustering trees. Available at arXiv:2106.02724.Google Scholar
Sainudiin, R., Stadler, T. and Véber, A. (2015). Finding the best resolution for the Kingman–Tajima coalescent: Theory and applications. J. Math. Biology 70, 1207–1247.CrossRefGoogle ScholarPubMed
Schweinsberg, J. (2002). An ${O}(n^{2})$ bound for the relaxation time of a Markov chain on cladograms. Random Structures Algorithms 20, 59–70.CrossRefGoogle Scholar
Spade, D., Herbei, R. and Kubatko, L. (2014). A note on the relaxation time of two Markov chains on rooted phylogenetic tree spaces. Statist. Prob. Lett. 84, 247–252.CrossRefGoogle Scholar
Stanley, R. P. (1999). Enumerative Combinatorics, Vol. I. Wadsworth & Brooks/Cole.Google Scholar
Štefankovič, D. and Vigoda, E. (2011). Fast convergence of Markov chain Monte Carlo algorithms for phylogenetic reconstruction with homogeneous data on closely related species. SIAM J. Discrete Math. 25, 1194–1211.CrossRefGoogle Scholar
Volz, E. M., Koelle, K. and Bedford, T. (2013). Viral phylodynamics. PLoS Comput. Biol. 9, e1002947.CrossRefGoogle ScholarPubMed
Wakeley, J. (2008). Coalescent Theory: An Introduction. Roberts.Google Scholar
Wilson, D. B. (2004). Mixing times of lozenge tiling and card shuffling Markov chains. Ann. Appl. Prob. 14, 274–325.CrossRefGoogle Scholar