Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-25T14:21:23.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Weak convergence of first passage time processes

Published online by Cambridge University Press:  14 July 2016

Ward Whitt
Ward Whitt*
Affiliation:
Yale University
Get access Rights & Permissions [Opens in a new window]

Extract

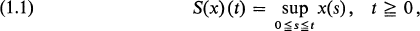Let D = D[0, ∞) be the space of all real-valued right-continuous functions on [0, ∞) with limits from the left. For any stochastic process X in D, let the associated supremum process be S(X), wherefor any x ∊ D. It is easy to verify that S: D → D is continuous in any of Skorohod's (1956) topologies extended from D[0,1] to D[0, ∞) (cf. Stone (1963) and Whitt (1970a, c)). Hence, weak convergence Xn ⇒ X in D implies weak convergence S(Xn) ⇒ S(X) in D by virtue of the continuous mapping theorem (cf. Theorem 5.1 of Billingsley (1968)).

Type
Short Communications
Information
Journal of Applied Probability , Volume 8 , Issue 2 , June 1971 , pp. 417 - 422
Copyright
Copyright © Applied Probability Trust 1971 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Billingsley, P. (1968) Convergence of Probability Measures. John Wiley and Sons, New York.Google Scholar
[2] Basu, A. K. (1969) On the asymptotic normality of the time of first passage over a curvilinear boundary. Queen's Mathematical Preprint, Queen's University, Kingston, Ontario.Google Scholar
[3] Breiman, L. (1967) First exit times from a square root boundary. Proc. Fifth Berkeley Symposium Math. Stat. Prob. 2, 9–16.Google Scholar
[4] Feller, W. (1949) Fluctuation theory of recurrent events. Trans. Amer. Math. Soc. 67, 98–119.Google Scholar
[5] Gani, J. and Prabhu, N. U. (1963) A storage model with continuous infinitely divisible inputs. Proc. Camb. Phil. Soc. 59, 417–429.Google Scholar
[6] Hasofer, A. M. (1964) A dam with inverse Gaussian input. Proc. Camb. Phil. Soc. 60, 931–933.Google Scholar
[7] Hooke, J. A. (1969) Some Limit Theorems for Priority Queues. Ph. D. Thesis, Cornell University. (Technical Report No. 91, Department of Operations Research, Cornell University).Google Scholar
[8] Iglehart, D. (1969) Diffusion approximations in collective risk theory. J. Appl. Prob. 6, 285–292.CrossRefGoogle Scholar
[9] Iglehart, D. and Whitt, W. (1969) The equivalence of functional central limit theorems for counting processes and associated partial sums. Technical Report No. 5, Department of Operations Research, Stanford University. To appear in Ann. Math. Statist. Google Scholar
[10] Ito, K. and Mckean, H. Jr. (1965) Diffusion Processes and Their Sample Paths. Springer-Verlag, Berlin.Google Scholar
[11] Kennedy, D. P. (1969) A functional central limit theorem for k-dimensional renewal theory. Technical Report No. 9, Department of Operations Research, Stanford University.Google Scholar
[12] Kennedy, D. P. (1970) Weak convergence for the superposition and thinning of point processes. Technical Report No. 11, Department of Operations Research, Stanford University.Google Scholar
[13] Moran, P. A. P. (1956) Probability theory of a dam with continuous release. Quart. J. Math. 27, 130–137.Google Scholar
[14] Prabhu, N. U. (1965) Queues and Inventories. John Wiley and Sons, New York.Google Scholar
[15] Roy, L. K. and Wasan, M. T. (1968a) Properties of the time distribution of standard Brownian motion. Queen's Mathematical Preprint No. 8, Queen's University, Kingston, Ontario.CrossRefGoogle Scholar
[16] Roy, L. K. and Wasan, M. T. (1968b) Some characteristic properties of the time distribution of standard Brownian motion. Queen's Mathematical Preprint No. 18, Queen's University, Kingston, Ontario.Google Scholar
[17] Roy, L. K. and Wasan, M. T. (1968) Tables of inverse Gaussian percentage points. Technometrics 11, 591–604.Google Scholar
[18] Siegmund, D. (1968) On the asymptotic normality of one-sided stopping rules. Ann. Math. Statist. 39, 1493–1497.CrossRefGoogle Scholar
[19] Skorohod, A. V. (1956) Limit theorems for stochastic processes. Theor. Probability Appl. 1, 262–290.Google Scholar
[20] Stone, C. (1963) Weak convergence of stochastic processes defined on semi-infinite time intervals. Proc. Amer. Math. Soc. 14, 694–696.CrossRefGoogle Scholar
[21] Tweedie, M. C. K. (1957a) Statistical properties of inverse Gaussian distributions, I. Ann. Math. Statist. 28, 362–377.Google Scholar
[22] Tweedie, M. C. K. (1957b) Statistical properies of inverse Gaussian distributions, II. Ann. Math. Statist. 28, 696–705.Google Scholar
[23] Wasan, M. T. (1968a) On an inverse Gaussian process. Skand. Aktuartidskr. 51, 69–96.Google Scholar
[24] Wasan, M. T. (1968b) Random functions from an inverse Gaussian process. Queen's Mathematical Preprints No. 5, Queen's University, Kingston, Ontario.Google Scholar
[25] Whitt, W. (1970a) Weak convergence of probability measures on the function space C[0, 8). Ann. Math. Statist. 41, 939–944.Google Scholar
[26] Whitt, W. (1970b) On functional central limit theorems in k-dimensional renewal theory. Technical Report, Department of Administrative Sciences, Yale University.Google Scholar
[27] Whitt, W. (1970c) Weak convergence of probability measures on the function space D[0, 8). Technical Report, Department of Administrative Sciences, Yale University.Google Scholar
[28] Whitt, W. (1971) Weak convergence theorems for priority queues: preemptive-resume discipline. J. Appl. Prob. 8, 74–94.Google Scholar