Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T13:40:33.452Z Has data issue: false hasContentIssue false
  • English
  • Français

Transient and slim versus recurrent and fat: Random walks and the trees they grow

Part of: Special processes Graph theory

Published online by Cambridge University Press:  01 October 2019

Giulio Iacobelli ,
Daniel R. Figueiredo  and
Giovanni Neglia
Giulio Iacobelli*
Affiliation:
Federal University of Rio de Janeiro
Daniel R. Figueiredo*
Affiliation:
Federal University of Rio de Janeiro
Giovanni Neglia*
Affiliation:
Inria, Université Côte d’Azur
*
* Postal address: Instituto de Matemática, Federal University of Rio de Janeiro, Rio de Janeiro, Brazil. Email address [email protected]
** Postal address: Department of Computer and System Engineering, COPPE, Federal University of Rio de Janeiro, Rio de Janeiro, Brazil. Email address [email protected]
*** Postal address: NEO Team, Inria, Sophia-Antipolis, France.Email address [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The no restart random walk (NRRW) is a random network growth model driven by a random walk that builds the graph while moving on it, adding and connecting a new leaf node to the current position of the walker every s steps. We show a fundamental dichotomy in NRRW with respect to the parity of s: for 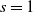${s}=1$ we prove that the random walk is transient and non-leaf nodes have degrees bounded above by an exponential distribution; for s even we prove that the random walk is recurrent and non-leaf nodes have degrees bounded below by a power law distribution. These theoretical findings highlight and confirm the diverse and rich behaviour of NRRW observed empirically.

Keywords

Random walkrandom graphnetwork growth model

MSC classification

Primary: 60K37: Processes in random environments
Secondary: 05C80: Random graphs 05C81: Random walks on graphs
Type
Research Papers
Information
Journal of Applied Probability , Volume 56 , Issue 3 , September 2019 , pp. 769 - 786
Copyright
© Applied Probability Trust 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amorim, B., Figueiredo, D., Iacobelli, G. and Neglia, G. (2016). Growing networks through random walks without restarts. In Complex Networks VII, eds Cherifi, H. et al., pp. 199–211. Springer.CrossRefGoogle Scholar
Angel, O., Crawford, N. and Kozma, G. (2014). Localization for linearly edge reinforced random walks. Duke Math. J . 163, 889–921.CrossRefGoogle Scholar
Barabási, A.-L. and Albert, R. (1999). Emergence of scaling in random networks. Science 286, 509–512.CrossRefGoogle ScholarPubMed
Campanino, M. and Petritis, D. (2014). Type transition of simple random walks on randomly directed regular lattices. J. Appl. Prob. 51, 1065–1080.CrossRefGoogle Scholar
Cannings, C. and Jordan, J. (2013). Random walk attachment graphs. Electron. Comm. Prob. 18, 1–5.CrossRefGoogle Scholar
Dembo, A., Huang, R. and Sidoravicius, V. (2014). Walking within growing domains: recurrence versus transience. Electron. J. Prob. 19, 1–20.CrossRefGoogle Scholar
Disertori, M., Sabot, C. and Tarrès, P. (2015). Transience of edge-reinforced random walk. Comm. Math. Phys. 339, 121–148.CrossRefGoogle Scholar
Figueiredo, D. R., Iacobelli, G., Oliveira, R. I., Reed, B. and Ribeiro, R. (2017). Building your path to escape from home. Available at arXiv:1709.10506.Google Scholar
Hoffman, C., Johnson, T. and Junge, M. (2016). From transience to recurrence with Poisson tree frogs. Ann. Appl. Prob. 26, 1620–1635.CrossRefGoogle Scholar
Ikeda, N. (2014). Network formed by movements of random walkers on a Bethe lattice. J. Phys. Conf. Series 490, 012189.CrossRefGoogle Scholar
Kumar, R., Novak, J. and Tomkins, A. (2010). Structure and evolution of online social networks. In Link Mining: Models, Algorithms, and Applications, eds Yu, P. S. et al., pp. 337–357. Springer.CrossRefGoogle Scholar
Li, M., Gao, L., Fan, Y., Wu, J. and Di, Z. (2010). Emergence of global preferential attachment from local interaction. New J. Phys . 12, 043029.CrossRefGoogle Scholar
Newman, M. (2018). Networks. Oxford University Press.CrossRefGoogle Scholar
Saramäki, J. and Kaski, K. (2004). Scale-free networks generated by random walkers. Phys. A Stat. Mech. Appl. 341, 80–86.CrossRefGoogle Scholar
Sporns, O. (2010). Networks of the Brain. MIT Press.CrossRefGoogle Scholar
Vázquez, A. (2003). Growing network with local rules: preferential attachment, clustering hierarchy, and degree correlations. Phys. Rev. E 67, 056104.CrossRefGoogle ScholarPubMed
Weng, L., Ratkiewicz, J., Perra, N., Gonçalves, B., Castillo, C., Bonchi, F., Schifanella, R., Menczer, F. and Flammini, A. (2013). The role of information diffusion in the evolution of social networks. In ACM International Conference on Knowledge Discovery and Data Mining (KDD), pp. 356–364. ACM.CrossRefGoogle Scholar