Published online by Cambridge University Press: 23 November 2020
For a spectrally negative self-similar Markov process on 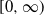 $[0,\infty)$ with an a.s. finite overall supremum, we provide, in tractable detail, a kind of conditional Wiener–Hopf factorization at the maximum of the absorption time at zero, the conditioning being on the overall supremum and the jump at the overall supremum. In a companion result the Laplace transform of this absorption time (on the event that the process does not go above a given level) is identified under no other assumptions (such as the process admitting a recurrent extension and/or hitting zero continuously), generalizing some existing results in the literature.
$[0,\infty)$ with an a.s. finite overall supremum, we provide, in tractable detail, a kind of conditional Wiener–Hopf factorization at the maximum of the absorption time at zero, the conditioning being on the overall supremum and the jump at the overall supremum. In a companion result the Laplace transform of this absorption time (on the event that the process does not go above a given level) is identified under no other assumptions (such as the process admitting a recurrent extension and/or hitting zero continuously), generalizing some existing results in the literature.