Article contents
Surprising identities for the greedy independent set on Cayley trees
Published online by Cambridge University Press: 25 August 2022
Abstract
We prove a surprising symmetry between the law of the size 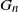 $G_n$
of the greedy independent set on a uniform Cayley tree
$G_n$
of the greedy independent set on a uniform Cayley tree 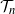 $ \mathcal{T}_n$
of size n and that of its complement. We show that
$ \mathcal{T}_n$
of size n and that of its complement. We show that 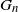 $G_n$
has the same law as the number of vertices at even height in
$G_n$
has the same law as the number of vertices at even height in 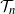 $ \mathcal{T}_n$
rooted at a uniform vertex. This enables us to compute the exact law of
$ \mathcal{T}_n$
rooted at a uniform vertex. This enables us to compute the exact law of 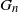 $G_n$
. We also give a Markovian construction of the greedy independent set, which highlights the symmetry of
$G_n$
. We also give a Markovian construction of the greedy independent set, which highlights the symmetry of 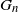 $G_n$
and whose proof uses a new Markovian exploration of rooted Cayley trees that is of independent interest.
$G_n$
and whose proof uses a new Markovian exploration of rooted Cayley trees that is of independent interest.
Keywords
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust
References
- 3
- Cited by



