Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-22T03:27:07.510Z Has data issue: false hasContentIssue false
  • English
  • Français

Sums of i.i.d. random variables and an application to the explosion criterion for markov branching processes

Published online by Cambridge University Press:  14 July 2016

H.-J. Schuh
H.-J. Schuh*
Affiliation:
University of Melbourne
*
∗Postal address: Department of Statistics, Richard Berry Building, University of Melbourne, Parkville, Vic 3052, Australia.
Get access Rights & Permissions [Opens in a new window]

Abstract

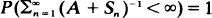We give necessary and sufficient conditions for in terms of 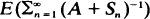, where Sn is the sum of n i.i.d. random variables with values in]0, ∞[, and A ≧ 0. We use these results to give a probabilistic proof of the ‘explosion criterion' for continuous-time Markov branching processes, which is usually shown analytically.

Keywords

SUMS OF I.I.D. RANDOM VARIABLESTAIL-SIGMA-FIELDSTOPPING TIMESTRONG LAW OF LARGE NUMBERSPROBABILITY GENERATING FUNCTIONSCONTINUOUS-TIME (TIME-HOMOGENEOUS) MARKOV BRANCHING PROCESSESEXPLOSION CRITERION
Type
Research Paper
Information
Journal of Applied Probability , Volume 19 , Issue 1 , March 1982 , pp. 29 - 38
Copyright
Copyright © Applied Probability Trust 1982 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Athreya, K. B. and Karlin, S. (1967) Limit theorems for the split times of branching processes. J. Math. Mech. 17, 257–277.Google Scholar
[2] Athreya, K. B. and Ney, P. E. (1972) Branching Processes. Springer-Verlag, Berlin.CrossRefGoogle Scholar
[3] Breiman, L. (1968) Probability. Addison-Wesley, Reading, Ma.Google Scholar
[4] Chung, K. L. (1960) Markov Chains with Stationary Transition Probabilities. Springer-Verlag, Berlin.CrossRefGoogle Scholar
[5] Harris, T. E. (1963) The Theory of Branching Processes. Springer-Verlag Berlin.CrossRefGoogle Scholar