Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Brockwell, P. J.
1970.
Stochastic population processes in the theory of radiative transfer.
Journal of Applied Probability,
Vol. 7,
Issue. 2,
p.
272.
Brockwell, P. J.
1970.
Stochastic population processes in the theory of radiative transfer.
Journal of Applied Probability,
Vol. 7,
Issue. 2,
p.
272.
Frigerio, Norman A.
1974.
Poisson and non-poisson behavior of radioactive systems.
Nuclear Instruments and Methods,
Vol. 114,
Issue. 1,
p.
175.
Libert, J.
1975.
Statistique de comptage: À propos d'une expérience récente.
Nuclear Instruments and Methods,
Vol. 126,
Issue. 4,
p.
589.
Teich, Malvin Carl
and
Vannucci, Giovanni
1978.
Observation of dead-time-modified photocounting distributions for modulated laser radiation.
Journal of the Optical Society of America,
Vol. 68,
Issue. 10,
p.
1338.
Jordan, D.R.
and
McBeth, G.W.
1978.
An experimental test of Müller statistics for counting systems with a non-extending dead time.
Nuclear Instruments and Methods,
Vol. 155,
Issue. 3,
p.
557.
Luthardt, M.
and
Prösch, U.
1980.
Zur Anwendbarkeit der Poissonverteilung bei radiochemischen Messungen.
Isotopenpraxis Isotopes in Environmental and Health Studies,
Vol. 16,
Issue. 9,
p.
288.
Opendak, M.
and
Wildenhain, P.
1994.
On the analysis of the decay of a small number of radioactive atoms in radiochemical solar neutrino experiments.
Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment,
Vol. 345,
Issue. 3,
p.
570.
Pál, Lénárd
and
Pázsit, Imre
2012.
On some problems in the counting statistics of nuclear particles.
Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment,
Vol. 693,
Issue. ,
p.
26.
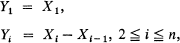 constitute a finite univariate population process as defined by Moyal [1], the individuals being the distances Yi with state space [0, x].
constitute a finite univariate population process as defined by Moyal [1], the individuals being the distances Yi with state space [0, x].