Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-25T15:07:45.588Z Has data issue: false hasContentIssue false
  • English
  • Français

Stochastic ordering for birth–death processes with killing

Part of: Distribution theory - Probability Markov processes

Published online by Cambridge University Press:  16 September 2021

Shoou-Ren Hsiau ,
May-Ru Chen  and
Yi-Ching Yao
Shoou-Ren Hsiau*
Affiliation:
National Changhua University of Education
May-Ru Chen*
Affiliation:
National Sun Yat-sen University
Yi-Ching Yao*
Affiliation:
Academia Sinica
*
*Postal address: Department of Mathematics, National Changhua University of Education, 1 Jin-De Road, Changhua 500, Taiwan, ROC. Email address: [email protected]
**Postal address: Department of Applied Mathematics, National Sun Yat-sen University, 70 Lien-hai Road, Kaohsiung 804, Taiwan, ROC. Email address: [email protected]
***Postal address: Institute of Statistical Science, Academia Sinica, 128 Academia Road, Section 2, Nankang, Taipei 11529, Taiwan, ROC. Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a birth–death process with killing where transitions from state i may go to either state 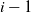$i-1$ or state 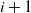$i+1$ or an absorbing state (killing). Stochastic ordering results on the killing time are derived. In particular, if the killing rate in state i is monotone in i, then the distribution of the killing time with initial state i is stochastically monotone in i. This result is a consequence of the following one for a non-negative tri-diagonal matrix M: if the row sums of M are monotone, so are the row sums of 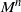$M^n$ for all 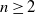$n\ge 2$ .

Keywords

Absorbing timeuniformizable chainbirth–death process with catastrophestri-diagonal matrix.

MSC classification

Primary: 60E15: Inequalities; stochastic orderings
Secondary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces) 60J27: Continuous-time Markov processes on discrete state spaces
Type
Original Article
Information
Journal of Applied Probability , Volume 58 , Issue 3 , September 2021 , pp. 708 - 720
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, W. J. (1991). Continuous-Time Markov Chains. Springer, New York.CrossRefGoogle Scholar
Brockwell, P. J. (1985). The extinction time of a birth, death and catastrophe process and a related diffusion model. Adv. Appl. Prob. 17, 42–52.CrossRefGoogle Scholar
Brockwell, P. J. (1986). The extinction time of a general birth and death process with catastrophes. J. Appl. Prob. 23, 851–858.CrossRefGoogle Scholar
Chao, X. and Zheng, Y. (2003). Transient analysis of immigration birth–death processes with total catastrophes. Prob. Eng. Inf. Sci. 17, 83–116.CrossRefGoogle Scholar
Chen, A., Zhang, H., Liu, K. and Rennolls, K. (2004). Birth–death processes with disasters and instantaneous resurrection. Adv. Appl. Prob. 36, 267–292.CrossRefGoogle Scholar
Di Crescenzo, A., Giorno, V., Nobile, A. G. and Ricciardi, L. M. (2008). A note on birth–death processes with catastrophes. Statist. Prob. Lett. 78, 2248–2257.CrossRefGoogle Scholar
Hadeler, K. P. (1986). Birth and death processes with killing and applications to parasitic infections. In Stochastic Spatial Processes (Lecture Notes Math. 1212), ed. Tautu, P., pp. 175–186. Springer, Heidelberg.Google Scholar
He, Q.-M. and Chavoushi, A. A. (2013). Analysis of queueing systems with customer interjections. Queueing Systems 73, 79–104.CrossRefGoogle Scholar
Irle, A. (2003). Stochastic ordering for continuous-time processes. J. Appl. Prob. 40, 361–375.CrossRefGoogle Scholar
Irle, A. and Gani, J. (2001). The detection of words and an ordering for Markov chains. J. Appl. Prob. 38A, 66–77.CrossRefGoogle Scholar
Karlin, S. and Tavaré, S. (1982). Linear birth and death processes with killing. J. Appl. Prob. 19, 477–487.CrossRefGoogle Scholar
Nagylaki, T. (2005). A stochastic model for a progressive chronic disease. J. Math. Biol. 51, 268–280.CrossRefGoogle ScholarPubMed
Puri, P. S. (1972). A method for studying the integral functionals of stochastic processes with applications III. In Proc. Sixth Berkeley Symp. Math. Stat. Prob., Vol. III, pp. 481–500. UCLA Press.Google Scholar
Resnick, S. I. (1992). Adventures in Stochastic Processes. Birkhäuser, Boston.Google Scholar
Ross, S. M. (2007). Introduction to Probability Models, 9th edn. Academic Press, New York.Google Scholar
Stirzaker, D. (2006). Processes with catastrophes. Math. Scientist 31, 107–118.Google Scholar
Van Doorn, E. A. and Zeifman, A. I. (2005). Birth–death processes with killing. Statist. Prob. Lett. 72, 33–42.CrossRefGoogle Scholar
Van Doorn, E. A. and Zeifman, A. I. (2005). Extinction probability in a birth–death process with killing. J. Appl. Prob. 42, 185–198.CrossRefGoogle Scholar