Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-09T05:51:33.114Z Has data issue: false hasContentIssue false
  • English
  • Français

Stochastic comparisons for fork-join queues with exponential processing times

Part of: Special processes

Published online by Cambridge University Press:  14 July 2016

Esther Frostig  and
Tapani Lehtonen
Esther Frostig*
Affiliation:
Haifa University
Tapani Lehtonen*
Affiliation:
Helsinki School of Economics
*
∗Postal address: Department of Statistics, Haifa University, Haifa, Israel, 31905.
∗∗Postal address: Helsinki School of Economics, Runebergink 14-16, 00100 Helsinki, Finland.
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider a fork-join queue, where each job upon arrival splits into k tasks and each joins a separate queue that is attended by a single server. Service times are independent, exponentially distributed random variables. Server i works at rate 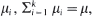, where μ is constant. We prove that the departure process becomes stochastically faster as the service rates become more homogeneous in the sense of stochastic majorization. Consequently, when all k servers work with equal rates the departure process is stochastically maximized.

Keywords

FORK-JOIN QUEUESSTOCHASTIC ORDERINGWEAK MAJORIZATION

MSC classification

Primary: 60K25: Queueing theory
Type
Research Article
Information
Journal of Applied Probability , Volume 34 , Issue 2 , June 1997 , pp. 487 - 497
Copyright
Copyright © Applied Probability Trust 1997 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Chang, C. S. (1992) A new ordering for stochastic majorization: theory and applications. Adv. Appl. Prob. 24, 604–634.Google Scholar
[2] Kamae, T., Krengel, U., O'Brien, G. L. (1977) Stochastic inequalities on partial ordered spaces. Ann. Prob. 5, 899–912.Google Scholar
[3] Lehtonen, T. (1986) On ordering of tandem queues with exponential servers. J Appl. Prob. 23, 115–129.Google Scholar
[4] Marshall, A. W. and Olkin, I. (1979) Inequalities: Theory of Majorization and its Applications. Academic Press, New York,Google Scholar
[5] Ross, S. M. (1983) Stochastic Processes. Wiley, New York.Google Scholar
[6] Stoyan, D. (1983) Comparison Methods for Queues and other Stochastic Models. Wiley, New York.Google Scholar
[7] Tsoucas, P. and Walrand, J. (1987) On the interchangeability and stochastic ordering of /M/1 queues in tandem. Adv. Appl. Prob. 19, 515–520.Google Scholar