Article contents
Stochastic approach to chemical kinetics
Published online by Cambridge University Press: 14 July 2016
Extract
In this article we shall present a summary of the various stochastic approaches and applications to chemical reaction kinetics, but before discussing these we first briefly introduce the basic ideas and definitions of classical or deterministic chemical kinetics. One of the basic questions to which chemists address themselves is the rate of chemical reactions, or in other words, how long it takes for a chemical reaction to attain completion, or equilibrium. Apparently the first significant quantitative investigation was made in 1850 by L. Wilhelmy [93]. He studied the inversion of sucrose (cane sugar) in aqueous solutions of acids, whose reaction is
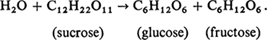 He found empirically that the rate of decrease of concentration of sucrose was simply proportional to the concentration remaining unconverted, i.e., if S(t) is the concentration of sucrose, then
He found empirically that the rate of decrease of concentration of sucrose was simply proportional to the concentration remaining unconverted, i.e., if S(t) is the concentration of sucrose, then
 The constant of proportionality is called the rate constant of the reaction. If So is the initial concentration of sucrose, then
The constant of proportionality is called the rate constant of the reaction. If So is the initial concentration of sucrose, then
 Since then an enormous number of reactions has been studied and the field of chemical kinetics is now one of the largest areas of chemical research. The importance of the field lies in the fact that it yields concise expressions for the time dependence of reactions, predicts yields, optimum economic conditions, and gives one much insight into the actual molecular processes involved. The detailed molecular picture of a reaction process is called the mechanism of the reaction.
Since then an enormous number of reactions has been studied and the field of chemical kinetics is now one of the largest areas of chemical research. The importance of the field lies in the fact that it yields concise expressions for the time dependence of reactions, predicts yields, optimum economic conditions, and gives one much insight into the actual molecular processes involved. The detailed molecular picture of a reaction process is called the mechanism of the reaction.
- Type
- Review Paper
- Information
- Copyright
- Copyright © Applied Probability Trust
References
- 613
- Cited by


