Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Weng, Wentao
and
Wang, Weina
2020.
Achieving Zero Asymptotic Queueing Delay for Parallel Jobs.
Proceedings of the ACM on Measurement and Analysis of Computing Systems,
Vol. 4,
Issue. 3,
p.
1.
Weng, Wentao
Zhou, Xingyu
and
Srikant, R.
2020.
Optimal Load Balancing with Locality Constraints.
Proceedings of the ACM on Measurement and Analysis of Computing Systems,
Vol. 4,
Issue. 3,
p.
1.
Weng, Wentao
and
Wang, Weina
2021.
Achieving Zero Asymptotic Queueing Delay for Parallel Jobs.
ACM SIGMETRICS Performance Evaluation Review,
Vol. 49,
Issue. 1,
p.
25.
Hellemans, Tim
and
Van Houdt, Benny
2021.
Mean Waiting Time in Large-Scale and Critically Loaded Power of d Load Balancing Systems.
ACM SIGMETRICS Performance Evaluation Review,
Vol. 49,
Issue. 1,
p.
53.
Hellemans, Tim
and
Van Houdt, Benny
2021.
Mean Waiting Time in Large-Scale and Critically Loaded Power of d Load Balancing Systems.
Proceedings of the ACM on Measurement and Analysis of Computing Systems,
Vol. 5,
Issue. 2,
p.
1.
Wang, Weina
Xie, Qiaomin
and
Harchol-Balter, Mor
2021.
Zero Queueing for Multi-Server Jobs.
Proceedings of the ACM on Measurement and Analysis of Computing Systems,
Vol. 5,
Issue. 1,
p.
1.
Hellemans, Tim
and
Van Houdt, Benny
2021.
Mean Waiting Time in Large-Scale and Critically Loaded Power of d Load Balancing Systems.
p.
53.
Hairi
Liu, Xin
and
Ying, Lei
2021.
Beyond Scaling.
p.
1.
Wang, Weina
Xie, Qiaomin
and
Harchol-Balter, Mor
2021.
Zero Queueing for Multi-Server Jobs.
p.
13.
Weng, Wentao
and
Wang, Weina
2021.
Achieving Zero Asymptotic Queueing Delay for Parallel Jobs.
p.
25.
Wang, Weina
Xie, Qiaomin
and
Harchol-Balter, Mor
2021.
Zero Queueing for Multi-Server Jobs.
ACM SIGMETRICS Performance Evaluation Review,
Vol. 49,
Issue. 1,
p.
13.
Liu, Xin
Gong, Kang
and
Ying, Lei
2022.
Large-System Insensitivity of Zero-Waiting Load Balancing Algorithms.
ACM SIGMETRICS Performance Evaluation Review,
Vol. 50,
Issue. 1,
p.
101.
Liu, Xin
Gong, Kang
and
Ying, Lei
2022.
Steady‐state analysis of load balancing with Coxian‐2 distributed service times.
Naval Research Logistics (NRL),
Vol. 69,
Issue. 1,
p.
57.
Hong, Yige
2022.
Sharp Zero-Queueing Bounds for Multi-Server Jobs.
ACM SIGMETRICS Performance Evaluation Review,
Vol. 49,
Issue. 2,
p.
66.
Bhamidi, Shankar
Budhiraja, Amarjit
and
Dewaskar, Miheer
2022.
Near equilibrium fluctuations for supermarket models with growing choices.
The Annals of Applied Probability,
Vol. 32,
Issue. 3,
Liu, Xin
and
Ying, Lei
2022.
Universal Scaling of Distributed Queues Under Load Balancing in the Super-Halfin-Whitt Regime.
IEEE/ACM Transactions on Networking,
Vol. 30,
Issue. 1,
p.
190.
Hong, Yige
and
Wang, Weina
2022.
Sharp waiting-time bounds for multiserver jobs.
p.
161.
Liu, Xin
Gong, Kang
and
Ying, Lei
2022.
Large-System Insensitivity of Zero-Waiting Load Balancing Algorithms.
p.
101.
der Boor, Mark Van
Borst, Sem C.
Van Leeuwaarden, Johan S. H.
and
Mukherjee, Debankur
2022.
Scalable Load Balancing in Networked Systems: A Survey of Recent Advances.
SIAM Review,
Vol. 64,
Issue. 3,
p.
554.
Varma, Sushil Mahavir
Castro, Francisco
and
Maguluri, Siva Theja
2023.
Power-of-d Choices Load Balancing in the Sub-Halfin Whitt Regime.
ACM SIGMETRICS Performance Evaluation Review,
Vol. 51,
Issue. 1,
p.
95.
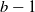 $b-1$ with
$b-1$ with  $b=O(\sqrt{\log N})$, i.e. a server can have at most one job in service and
$b=O(\sqrt{\log N})$, i.e. a server can have at most one job in service and 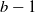 $b-1$ jobs queued. We focus on the steady-state performance of load-balancing algorithms in the heavy traffic regime such that the load of the system is
$b-1$ jobs queued. We focus on the steady-state performance of load-balancing algorithms in the heavy traffic regime such that the load of the system is 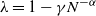 $\lambda = 1 - \gamma N^{-\alpha}$ for
$\lambda = 1 - \gamma N^{-\alpha}$ for 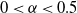 $0<\alpha<0.5$ and
$0<\alpha<0.5$ and 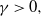 $\gamma > 0,$ which we call the sub-Halfin–Whitt regime (
$\gamma > 0,$ which we call the sub-Halfin–Whitt regime (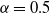 $\alpha=0.5$ is the so-called Halfin–Whitt regime). We establish a sufficient condition under which the probability that an incoming job is routed to an idle server is 1 asymptotically (as
$\alpha=0.5$ is the so-called Halfin–Whitt regime). We establish a sufficient condition under which the probability that an incoming job is routed to an idle server is 1 asymptotically (as 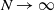 $N \to \infty$) at steady state. The class of load-balancing algorithms that satisfy the condition includes join-the-shortest-queue, idle-one-first, join-the-idle-queue, and power-of-d-choices with
$N \to \infty$) at steady state. The class of load-balancing algorithms that satisfy the condition includes join-the-shortest-queue, idle-one-first, join-the-idle-queue, and power-of-d-choices with 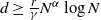 $d\geq \frac{r}{\gamma}N^\alpha\log N$ (r a positive integer). The proof of the main result is based on the framework of Stein’s method. A key contribution is to use a simple generator approximation based on state space collapse.
$d\geq \frac{r}{\gamma}N^\alpha\log N$ (r a positive integer). The proof of the main result is based on the framework of Stein’s method. A key contribution is to use a simple generator approximation based on state space collapse.