Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T14:43:00.103Z Has data issue: false hasContentIssue false
  • English
  • Français

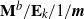Simple analytical solutions for the $\mathbf{M}^{b}/\mathbf{E}_{k}/1/\textbf{m}$, 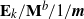$\mathbf{E}_{k}/\mathbf{M}^{b}/1/\textbf{m}$, and related queues

Part of: Special processes Computer system organization

Published online by Cambridge University Press:  18 August 2022

Benny Van Houdt Open the ORCID record for Benny Van Houdt [Opens in a new window]
Benny Van Houdt*
Affiliation:
University of Antwerp
*
*Postal address: Middelheimlaan 1, B2020 Antwerp, Belgium. Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we revisit some classical queueing systems such as the M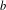 $^b$ /E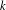 $_k$ /1/m and E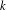 $_k$ /M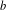 $^b$ /1/m queues, for which fast numerical and recursive methods exist to study their main performance measures. We present simple explicit results for the loss probability and queue length distribution of these queueing systems as well as for some related queues such as the M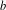 $^b$ /D/1/m queue, the D/M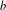 $^b$ /1/m queue, and fluid versions thereof. In order to establish these results we first present a simple analytical solution for the invariant measure of the M/E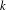 $_k$ /1 queue that appears to be new.

Keywords

Queueing systemsanalytical solutionloss probabilitybulk servicebulk arrivalsErlang-k distribution

MSC classification

Primary: 60K25: Queueing theory
Secondary: 68M20: Performance evaluation; queueing; scheduling
Type
Original Article
Information
Journal of Applied Probability , Volume 59 , Issue 4 , December 2022 , pp. 1129 - 1143
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adan, I. and Resing, J. (2001). Queueing Theory: Ivo Adan and Jacques Resing. Department of Mathematics and Computing Science, Eindhoven University of Technology.Google Scholar
Asmussen, S. (2008). Applied Probability and Queues (Stochastic Modelling and Applied Probability 51). Springer Science & Business Media.Google Scholar
Brun, O. and Garcia, J.-M. (2000). Analytical solution of finite capacity M/D/1 queues. J. Appl. Prob. 37, 1092–1098.CrossRefGoogle Scholar
Gross, D. and Harris, C. (1974). Fundamentals of Queueing Theory. John Wiley, New York.Google Scholar
Hellemans, T., Kielanski, G. and Van Houdt, B. (2022). Performance of load balancers with bounded maximum queue length in case of non-exponential job sizes. Available at arXiv:2201.03905.Google Scholar
Kleinrock, L. (1975). Queueing Systems, Vol. I. Wiley, New York.Google Scholar
Kleinrock, L. (1976). Queueing Systems, Vol. II. Wiley, New York.Google Scholar
Latouche, G. and Ramaswami, V. (1999). Introduction to Matrix Analytic Methods and Stochastic Modeling. SIAM, Philadelphia.CrossRefGoogle Scholar
Medhi, J. (2002). Stochastic Models in Queueing Theory. Elsevier.Google Scholar
Miyazawa, M. (1990). Complementary generating functions for the M $^X$ /GI/1/k and GI/M $^Y$ /1/k queues and their application to the comparison of loss probabilities. J. Appl. Prob. 27, 684–692.CrossRefGoogle Scholar
Miyazawa, M. and Shanthikumar, J. G. (1991). Monotonicity of the loss probabilities of single server finite queues with respect to convex order of arrival or service processes. Prob. Eng. Inf. Sci. 5, 43–52.CrossRefGoogle Scholar
Neuts, M. (1981). Matrix-Geometric Solutions in Stochastic Models: An Algorithmic Approach. Johns Hopkins University Press.Google Scholar
Neuts, M. (1989). Structured Stochastic Matrices of M/G/1 Type and their Applications . Marcel Dekker, New York and Basel.Google Scholar
Tsitsiklis, J. N. and Xu, K. (2012). On the power of (even a little) resource pooling. Stoch. Syst. 2, 1–66.CrossRefGoogle Scholar