Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-11T02:42:23.076Z Has data issue: false hasContentIssue false
  • English
  • Français

Short-time behavior of solutions to Lévy-driven stochastic differential equations

Part of: Stochastic processes Stochastic analysis

Published online by Cambridge University Press:  12 January 2023

Jana Reker
Jana Reker*
Affiliation:
Ulm University
*
*Postal address:Ulm University, Institute of Mathematical Finance, Helmholtzstraße 18, 89081 Ulm, Germany. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider solutions of Lévy-driven stochastic differential equations of the form 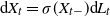$\textrm{d} X_t=\sigma(X_{t-})\textrm{d} L_t$, 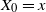$X_0=x$, where the function $\sigma$ is twice continuously differentiable and the driving Lévy process 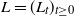$L=(L_t)_{t\geq0}$ is either vector or matrix valued. While the almost sure short-time behavior of Lévy processes is well known and can be characterized in terms of the characteristic triplet, there is no complete characterization of the behavior of the solution X. Using methods from stochastic calculus, we derive limiting results for stochastic integrals of the form 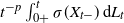$t^{-p}\int_{0+}^t\sigma(X_{t-})\,\textrm{d} L_t$ to show that the behavior of the quantity 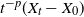$t^{-p}(X_t-X_0)$ for 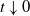$t\downarrow0$ almost surely reflects the behavior of 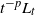$t^{-p}L_t$. Generalizing 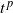$t^{{\kern1pt}p}$ to a suitable function 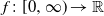$f\colon[0,\infty)\rightarrow\mathbb{R}$ then yields a tool to derive explicit law of the iterated logarithm type results for the solution from the behavior of the driving Lévy process.

Keywords

Short-time behaviorLévy-driven SDELIL-type results

MSC classification

Primary: 60G17: Sample path properties
Secondary: 60G51: Processes with independent increments; L'evy processes 60H20: Stochastic integral equations
Type
Original Article
Information
Journal of Applied Probability , Volume 60 , Issue 3 , September 2023 , pp. 765 - 780
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bertoin, J. (1996). Lévy Processes. Cambridge University Press.Google Scholar
Bertoin, J., Doney, R. A. and Maller, R. A. (2008). Passage of Lévy processes across power law boundaries at small times. Ann. Prob. 36, 160–197.10.1214/009117907000000097CrossRefGoogle Scholar
Blumenthal, S. M. and Getoor, R. K. (1961). Sample functions of stochastic processes with stationary independent increments. J. Math. Mech. 10, 493–516.Google Scholar
de Weert, F. J. (2003). Attraction to stable distributions for Lévy processes at zero. MPhil thesis, University of Manchester.Google Scholar
Doney, R. A. and Maller, R. A. (2002) Stability and attraction to normality for Lévy processes at zero and at infinity. J. Theor. Prob. 15, 751–792.10.1023/A:1016228101053CrossRefGoogle Scholar
Einmahl, U. (2019) LIL-type behaviour of multivariate Lévy processes at zero. Trans. Amer. Math. Soc. 372, 6437–6464.10.1090/tran/7805CrossRefGoogle Scholar
Karandikar, R. L. (1991) Multiplicative decomposition of nonsingular matrix valued semimartingales. In Séminaire de probabilités (Lect. Notes Math. 1485). Springer, New York, pp. 262–269.10.1007/BFb0100860CrossRefGoogle Scholar
Knopova, V. and Schilling, R. (2014). On the small-time behaviour of Lévy-type processes. Stoch. Process. Appl. 124, 2249–2265.CrossRefGoogle Scholar
Kühn, F. (2018) Solutions of Lévy-driven SDEs with unbounded coefficients as Feller processes. Proc. Amer. Math. Soc. 146, 3591–3604.Google Scholar
Kühn, F. (2021) Upper functions for sample paths of Lévy(-type) processes. Preprint, arXiv:2102.06541.Google Scholar
Maller, R. A. and Mason, D. M. (2008) Convergence in distribution of Lévy processes at small times with self-normalization. Acta. Sci. Math. (Szeged) 74, 315–347.Google Scholar
Protter, P. (2005) Stochastic Integration and Differential Equations, 2nd edn. Springer, Berlin.10.1007/978-3-662-10061-5CrossRefGoogle Scholar
Pruitt, W. E. (1981). The growth of random walks and Lévy processes. Ann. Prob. 9, 948–956.10.1214/aop/1176994266CrossRefGoogle Scholar
Rogozin, B. A. (1968). Local behaviour of processes with independent increments. Theory Prob. Appl. 13, 482–486.10.1137/1113059CrossRefGoogle Scholar
Sato, K. (2013). Lévy Processes and Infinitely Divisible Distributions, 2nd edn. Cambridge University Press.Google Scholar
Savov, M. S. (2009). Small time two-sided LIL behavior for Lévy processes at zero. Prob. Theory Relat. Fields 144, 79–98.10.1007/s00440-008-0142-1CrossRefGoogle Scholar
Savov, M. S. (2010). Small time one-sided LIL behavior for Lévy processes at zero. J. Theor. Prob. 23, 209–236.CrossRefGoogle Scholar
Schilling, R. and Schnurr, A. (2010). The symbol associated with the solution of a stochastic differential equation. Electron. J. Prob. 15, 1369–1393.10.1214/EJP.v15-807CrossRefGoogle Scholar
Schnurr, A. (2013) Generalization of the Blumenthal–Getoor index to the class of homogeneous diffusions with jumps and some applications. Bernoulli 19, 2010–2032.10.3150/12-BEJ441CrossRefGoogle Scholar
Shtatland, E. S. (1965). On local properties of processes with independent increments. Theory Prob. Appl. 10, 317–322.10.1137/1110036CrossRefGoogle Scholar