Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Davison, A. C.
1988.
Approximate Conditional Inference in Generalized Linear Models.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 50,
Issue. 3,
p.
445.
Barndorff-Nielsen, O. E.
and
Cox, D. R.
1989.
Asymptotic Techniques for Use in Statistics.
p.
220.
Dinges, H.
1989.
Special cases of second order Wiener germ approximations.
Probability Theory and Related Fields,
Vol. 83,
Issue. 1-2,
p.
5.
Minkin, Salomon
1989.
Statistical Modelling.
Vol. 57,
Issue. ,
p.
234.
Wang, Suojin
1990.
Saddlepoint approximations for bivariate distributions.
Journal of Applied Probability,
Vol. 27,
Issue. 03,
p.
586.
Wang, Soujin
1990.
Saddlepoint approximations for nonlinear statistics.
Canadian Journal of Statistics,
Vol. 18,
Issue. 3,
p.
255.
Jensen, Jens Ledet
1991.
Uniform Saddlepoint Approximations and Log-Concave Densities.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 53,
Issue. 1,
p.
157.
Pierce, Donald A.
and
Peters, Dawn
1992.
Practical Use of Higher Order Asymptotics for Multiparameter Exponential Families.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 54,
Issue. 3,
p.
701.
1992.
Discussion of the Paper by Pierce and Peters.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 54,
Issue. 3,
p.
725.
Wood, Andrew T. A.
Booth, James G.
and
Butler, Ronald W.
1993.
Saddlepoint Approximations to the CDF of Some Statistics with Nonnormal Limit Distributions.
Journal of the American Statistical Association,
Vol. 88,
Issue. 422,
p.
680.
Wang, Suojin
1993.
Saddlepoint approximations in conditional inference.
Journal of Applied Probability,
Vol. 30,
Issue. 02,
p.
397.
Butler, Ronald W.
Huzurbazar, S.
and
Booth, James G.
1993.
Saddlepoint Approximations for Tests of Block Independence, Sphericity and Equal Variances and Covariances.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 55,
Issue. 1,
p.
171.
1993.
Discussion on the Meeting on the Gibbs Sampler and Other Markov Chain Monte Carlo Methods.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 55,
Issue. 1,
p.
53.
Agresti, Alan
Lang, Joseph B.
and
Mehta, Cyrus.
1993.
Some empirical comparisons of exact, modified exact, and higher-order asymptotic tests of independence for ordered categorical variables.
Communications in Statistics - Simulation and Computation,
Vol. 22,
Issue. 1,
p.
1.
Kolassa, John E.
and
Tanner, Martin A.
1994.
Approximate Conditional Inference in Exponential Families via the Gibbs Sampler.
Journal of the American Statistical Association,
Vol. 89,
Issue. 426,
p.
697.
Wong, A.C.M.
1995.
A simple and accurate inference procedure for the difference of failure intensities from two exponential distributions.
Communications in Statistics - Theory and Methods,
Vol. 24,
Issue. 11,
p.
2865.
Booth, James G.
Butler, Ronald W.
Huzurbazar, S.
and
Wood, Andrew T.A.
1995.
Saddlepoint approximations for P-values of some tests of covariance matrices.
Journal of Statistical Computation and Simulation,
Vol. 53,
Issue. 3-4,
p.
165.
Wang, Suojin
1995.
One-step saddlepoint approximations for quantiles.
Computational Statistics & Data Analysis,
Vol. 20,
Issue. 1,
p.
65.
Barndorff-Nielsen, Ole E.
and
Schmidli, Hanspeter
1995.
Saddlepoint approximations for the probability of ruin in finite time.
Scandinavian Actuarial Journal,
Vol. 1995,
Issue. 2,
p.
169.
Strawderman, Robert L.
Casella, George
and
Wells, Martin T.
1996.
Practical Small-Sample Asymptotics for Regression Problems.
Journal of the American Statistical Association,
Vol. 91,
Issue. 434,
p.
643.
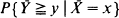 where
where 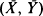 is an average of n independent bivariate random vectors. A more general version, corresponding to the conditioning on a p – 1-dimensional linear function of a p-dimensional variable is also included. A separate formula is given for the lattice case. The expansion is a generalization of the Lugannani and Rice (1980) formula, which reappears if
is an average of n independent bivariate random vectors. A more general version, corresponding to the conditioning on a p – 1-dimensional linear function of a p-dimensional variable is also included. A separate formula is given for the lattice case. The expansion is a generalization of the Lugannani and Rice (1980) formula, which reappears if 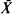 and
and 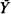 are independent. As an example an approximation to the hypergeometric distribution is derived.
are independent. As an example an approximation to the hypergeometric distribution is derived.