Published online by Cambridge University Press: 28 February 2023
Let 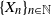 $\{X_n\}_{n\in{\mathbb{N}}}$ be an
$\{X_n\}_{n\in{\mathbb{N}}}$ be an 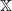 ${\mathbb{X}}$-valued iterated function system (IFS) of Lipschitz maps defined as
${\mathbb{X}}$-valued iterated function system (IFS) of Lipschitz maps defined as 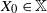 $X_0 \in {\mathbb{X}}$ and for
$X_0 \in {\mathbb{X}}$ and for 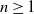 $n\geq 1$,
$n\geq 1$, 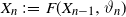 $X_n\;:\!=\;F(X_{n-1},\vartheta_n)$, where
$X_n\;:\!=\;F(X_{n-1},\vartheta_n)$, where 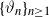 $\{\vartheta_n\}_{n \ge 1}$ are independent and identically distributed random variables with common probability distribution
$\{\vartheta_n\}_{n \ge 1}$ are independent and identically distributed random variables with common probability distribution 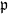 $\mathfrak{p}$,
$\mathfrak{p}$, 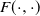 $F(\cdot,\cdot)$ is Lipschitz continuous in the first variable, and
$F(\cdot,\cdot)$ is Lipschitz continuous in the first variable, and 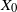 $X_0$ is independent of
$X_0$ is independent of 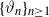 $\{\vartheta_n\}_{n \ge 1}$. Under parametric perturbation of both F and
$\{\vartheta_n\}_{n \ge 1}$. Under parametric perturbation of both F and 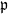 $\mathfrak{p}$, we are interested in the robustness of the V-geometrical ergodicity property of
$\mathfrak{p}$, we are interested in the robustness of the V-geometrical ergodicity property of 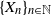 $\{X_n\}_{n\in{\mathbb{N}}}$, of its invariant probability measure, and finally of the probability distribution of
$\{X_n\}_{n\in{\mathbb{N}}}$, of its invariant probability measure, and finally of the probability distribution of 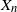 $X_n$. Specifically, we propose a pattern of assumptions for studying such robustness properties for an IFS. This pattern is implemented for the autoregressive processes with autoregressive conditional heteroscedastic errors, and for IFS under roundoff error or under thresholding/truncation. Moreover, we provide a general set of assumptions covering the classical Feller-type hypotheses for an IFS to be a V-geometrical ergodic process. An accurate bound for the rate of convergence is also provided.
$X_n$. Specifically, we propose a pattern of assumptions for studying such robustness properties for an IFS. This pattern is implemented for the autoregressive processes with autoregressive conditional heteroscedastic errors, and for IFS under roundoff error or under thresholding/truncation. Moreover, we provide a general set of assumptions covering the classical Feller-type hypotheses for an IFS to be a V-geometrical ergodic process. An accurate bound for the rate of convergence is also provided.