Published online by Cambridge University Press: 02 September 2022
Let
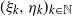 $(\xi_k,\eta_k)_{k\in\mathbb{N}}$
be independent identically distributed random vectors with arbitrarily dependent positive components. We call a (globally) perturbed random walk a random sequence
$(\xi_k,\eta_k)_{k\in\mathbb{N}}$
be independent identically distributed random vectors with arbitrarily dependent positive components. We call a (globally) perturbed random walk a random sequence
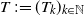 $T\,{:\!=}\, (T_k)_{k\in\mathbb{N}}$
defined by
$T\,{:\!=}\, (T_k)_{k\in\mathbb{N}}$
defined by
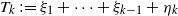 $T_k\,{:\!=}\, \xi_1+\cdots+\xi_{k-1}+\eta_k$
for
$T_k\,{:\!=}\, \xi_1+\cdots+\xi_{k-1}+\eta_k$
for
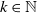 $k\in\mathbb{N}$
. Consider a general branching process generated by T and let
$k\in\mathbb{N}$
. Consider a general branching process generated by T and let
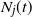 $N_j(t)$
denote the number of the jth generation individuals with birth times
$N_j(t)$
denote the number of the jth generation individuals with birth times
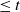 $\leq t$
. We treat early generations, that is, fixed generations j which do not depend on t. In this setting we prove counterparts for
$\leq t$
. We treat early generations, that is, fixed generations j which do not depend on t. In this setting we prove counterparts for
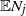 $\mathbb{E}N_j$
of the Blackwell theorem and the key renewal theorem, prove a strong law of large numbers for
$\mathbb{E}N_j$
of the Blackwell theorem and the key renewal theorem, prove a strong law of large numbers for
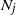 $N_j$
, and find the first-order asymptotics for the variance of
$N_j$
, and find the first-order asymptotics for the variance of
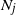 $N_j$
. Also, we prove a functional limit theorem for the vector-valued process
$N_j$
. Also, we prove a functional limit theorem for the vector-valued process
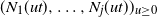 $(N_1(ut),\ldots, N_j(ut))_{u\geq0}$
, properly normalized and centered, as
$(N_1(ut),\ldots, N_j(ut))_{u\geq0}$
, properly normalized and centered, as
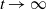 $t\to\infty$
. The limit is a vector-valued Gaussian process whose components are integrated Brownian motions.
$t\to\infty$
. The limit is a vector-valued Gaussian process whose components are integrated Brownian motions.