Published online by Cambridge University Press: 14 July 2016
In this study an asymptotical analysis of the reliability of a complex renewable system with an unbounded number of repair units is provided. The system state is given by a binary vector e(t) = [e1(t), · ··, en(t)], ei(t) = 0(1), if at moment t the ith element is failure-free (failed). We assume that at the state e the ith element has failure intensity λi(e). At the instant of failure of every element the renewal work begins and the renewal time has distribution function Gi(t). Let E_ be the set of failed system states. The goal of this study is the asymptotic estimation of the distribution of the time until the first system failure, 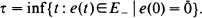 .
.