Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T12:54:09.299Z Has data issue: false hasContentIssue false
  • English
  • Français

Regression for randomly sampled spatial series: the trigonometric case

Published online by Cambridge University Press:  14 July 2016

David R. Brillinger
Get access Rights & Permissions [Opens in a new window]

Abstract

The model Y(t) = s(t | θ) + ε(t) is studied in the case that observations are made at scattered points τ j in a subset of Rp and θ is a finite-dimensional parameter. The particular cases of 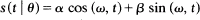0 = (α, β) and (α, β, ω) are considered in detail. Consistency and asymptotic normality results are developed assuming that the spatial series ε(·) and the point process {τ j} are independent, stationary and mixing. The estimates considered are equivalent to least squares asymptotically and are not generally asymptotically efficient.

Contributions of the paper include: study of the Rp case, management of irregularly placed observations, allowance for abnormal domains of observation and the discovery that aliasing complications do not arise when the point process {τ j} is mixing. There is a brief discussion of the construction and properties of maximum likelihood estimates for the spatial-temporal case.

Keywords

POINT PROCESSPROCESS WITH STATIONARY INCREMENTSNON-LINEAR REGRESSIONTRIGONOMETRIC REGRESSIONPERIODOGRAMRANDOM MEASUREHIDDEN PERIODICITIESARRAY DATABLUE
Type
Part 5—Random Fields and Point Processes
Information
Journal of Applied Probability , Volume 23 , Issue A: Essays in Time Series and Allied Processes , 1986 , pp. 275 - 289
Copyright
Copyright © 1986 Applied Probability Trust 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brillinger, D. R. (1970) The frequency analysis of relations between stationary spatial series. In Proc. Twelfth Bien. Sem. Canadian Math. Congr. , ed. Pyke, R. Canadian Mathematical Congress, Montreal, 39–81.Google Scholar
Brillinger, D. R. (1972) The spectral analysis of stationary interval functions. Proc. 6th Berkeley Symp. Math. Statist. Prob. 1, 483–513.Google Scholar
Brillinger, D. R. (1973) Estimation of the mean of a stationary time series by sampling. J. Appl. Prob. 10, 419–431.Google Scholar
Brillinger, D. R. (1975) Time Series: Data Analysis and Theory. Holt, Rinehart and Winston, New York.Google Scholar
Brillinger, D. R. (1983) The finite Fourier transform of a stationary process. In Handbook of Statistics 3, ed. Brillinger, D. R. and Krishnaiah, P. R., North-Holland, Amsterdam, 21–38.Google Scholar
Capon, J. (1969) High resolution frequency-wavenumber spectrum analysis. Proc. IEEE 57, 1408–1418.Google Scholar
Chiang, T-P. (1959) On the estimation of regression coefficients of a continuous parameter time series with a stationary residual. Theory Prob. Appl. 4, 373–390.Google Scholar
Dunsmuir, W. (1984) Large sample properties of estimation in time series observed at unequally spaced times. In Proc. Symp. Time Series Analysis of Irregularly Observed Data , ed. Parzen, E. Springer-Verlag, New York.Google Scholar
Edwards, R. E. (1965) Functional Analysis. Holt, Rinehart and Winston, New York.Google Scholar
Geisser, S. (1980) Growth curve analysis. In Handbook of Statistics , 1, ed. Krishnaiah, P. R., North-Holland, Amsterdam, 89–116.Google Scholar
Grenander, U. (1954) On the estimation of regression coefficients in the case of autocorrelated disturbance. Ann. Math. Statist. 25, 252–272.Google Scholar
Grenander, U. and Rosenblatt, M. (1957) Statistical Analysis of Stationary Time Series. Wiley, New York.Google Scholar
Hannan, E. J. (1970) Multiple Time Series. Wiley, New York.Google Scholar
Hannan, E. J. (1971) Non-linear time series regression. J. Appl. Prob. 8, 767–780.CrossRefGoogle Scholar
Hannan, E. J. (1973) The estimation of frequency. J. Appl. Prob. 10, 510–519.CrossRefGoogle Scholar
Hannan, E. J. (1975) Linear regression in continuous time. J. Austral. Math. Soc. 19, 146–159.Google Scholar
Hinich, M. J. and Shaman, P. (1972) Parameter estimation for an R-dimensional plane wave observed with additive independent Gaussian errors. Ann. Math. Statist. 43, 153–169.Google Scholar
Isokawa, Y. (1983) Estimation of frequency by random sampling. Ann. Inst. Statist. Math. 35, 201–213.Google Scholar
Ivanov, A. V. (1980) A solution of the problem of detecting hidden periodicities. Theory Prob. Math. Statist. 20, 51–68.Google Scholar
Khatri, C. G. (1966) A note on a MANOVA model applied to problems in growth curve. Ann. Inst. Statist. Math. 18, 75–86.Google Scholar
Kholevo, A. S. (1969) On estimates of regression coefficients. Theory Prob. Appl. 14, 79–104.Google Scholar
Kholevo, A. S. (1971) Almost-periodic signal estimation. Theory Prob. Appl. 16, 249–263.CrossRefGoogle Scholar
Kutoyants, Yu. A. (1977) Estimation of a parameter of a signal in Guassian noise. Probi. Pered. Inform. 13, 29–36.Google Scholar
Leonenko, N. N. (1981) On the invariance principle for estimators of linear regression coefficients of a random field. Theory Prob. Math. Statist. 23, 87–96.Google Scholar
Masry, E. (1980) Discrete-time spectral estimation of continuous-time processes–the orthogonal series method. Ann. Statist. 5, 1100–1109.Google Scholar
Mcdunnough, P. and Wolfson, D. B. (1979) On some sampling schemes for estimating the parameters of a continuous time series. Ann. Inst. Statist. Math. 31, 487–497.Google Scholar
Pisarenko, V. F. (1973) Estimation of parameters of two harmonics of close frequencies on a background of noise. Theory Prob. Appl. 18, 826.Google Scholar
Roberts, J. B. and Gaster, M. (1980) On the estimation of spectra from randomly sampled signals; a method of reducing variability. Proc. R. Soc. London 371, 235–258.Google Scholar
Robinson, P. M. (1972) Non-linear regression for multiple time-series. J. Appl. Prob. 9, 758–768.Google Scholar
Shumway, R. H. (1983) Replicated time-series regression: an approach to signal estimation and detection. In Handbook of Statistics 3, ed. Brillinger, D. R. and Krishnaiah, P. R., North-Holland, Amsterdam, 383–408.Google Scholar
Timan, A. F. (1963) Theory of Approximation of Functions of a Real Variable. Pergamon, Oxford.Google Scholar
Vere-Jones, D. (1982) On the estimation of frequency in point process data. Essays in Statistical Science , ed. Gani, J. and Hannan, E. J., Applied Probability Trust, Sheffield, 383–394.Google Scholar
Walker, A. M. (1971) On the estimation of a harmonic component in a times series with stationary independent residuals. Biometrika 58, 21–36.Google Scholar
Walker, A. M. (1973) On the estimation of a harmonic component in a time series with stationary dependent residuals. Adv. Appl. Prob. 5, 217–241.Google Scholar
Whittle, P. (1952). The simultaneous estimation of a time series' harmonic components and covariance structure. Trab. Estadist. 3, 43–57.CrossRefGoogle Scholar