Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-27T06:49:04.088Z Has data issue: false hasContentIssue false
  • English
  • Français

Regeneration of branching processes with immigration in varying environments

Part of: Markov processes

Published online by Cambridge University Press:  21 November 2024

Hong-Yan Sun ,
Hua-Ming Wang ,
Bao-Zhi Li  and
Hui Yang
Hong-Yan Sun*
Affiliation:
China University of Geosciences
Hua-Ming Wang*
Affiliation:
Anhui Normal University
Bao-Zhi Li*
Affiliation:
Anhui Normal University
Hui Yang*
Affiliation:
Minzu University of China
*
*Postal address: School of Sciences, China University of Geosciences, Beijing 100083, China. Email: [email protected]
**Postal address: School of Mathematics and Statistics, Anhui Normal University, Wuhu 241003, China.
**Postal address: School of Mathematics and Statistics, Anhui Normal University, Wuhu 241003, China.
***Postal address: School of Sciences, Minzu University of China, Beijing 100081, China.
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider linear-fractional branching processes (one-type and two-type) with immigration in varying environments. For 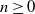$n\ge0$, let 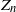$Z_n$ count the number of individuals of the nth generation, which excludes the immigrant who enters the system at time n. We call n a regeneration time if 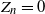$Z_n=0$. For both the one-type and two-type cases, we give criteria for the finiteness or infiniteness of the number of regeneration times. We then construct some concrete examples to exhibit the strange phenomena caused by the so-called varying environments. For example, it may happen that the process is extinct, but there are only finitely many regeneration times. We also study the asymptotics of the number of regeneration times of the model in the example.

Keywords

Branching processesimmigrationregeneration timescontinued fractionsproduct of nonnegative matrices

MSC classification

Primary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.)
Secondary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Type
Original Article
Information
Journal of Applied Probability , Volume 62 , Issue 1 , March 2025 , pp. 422 - 444
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Agresti, A. (1975). On the extinction times of varying and random environment branching processes. J. Appl. Prob. 12, 39–46.CrossRefGoogle Scholar
Athreya, K. B. and Ney, P. E. (1972). Branching Processes. Springer, New York.CrossRefGoogle Scholar
Bhattacharya, N. and Perlman, M. (2017). Time inhomogeneous branching processes conditioned on non-extinction. Preprint, arXiv:1703.00337 [math.PR].Google Scholar
Biggins, J. D., Cohn, H. and Nerman, O. (1999). Multi-type branching in varying environment. Stoch. Process. Appl. 83, 357–400.CrossRefGoogle Scholar
Cohn, H. and Wang, Q. (2003). Multitype branching limit behavior. Ann. Appl. Prob. 13, 490–500.CrossRefGoogle Scholar
Csáki, E., Földes, A. and Révész, P. (2010). On the number of cutpoints of the transient nearest neighbor random walk on the line. J. Theoret. Prob. 23, 624–638.CrossRefGoogle Scholar
Dolgopyat, D., Hebbar, P., Koralov, L. and Perlman, M. (2018). Multi-type branching processes with time-dependent branching rates. J. Appl. Prob. 55, 701–727.CrossRefGoogle Scholar
Fazekas, I. and Klesov, O. (2001). A general approach to the strong law of large numbers. Theory Prob. Appl. 45, 436–449.CrossRefGoogle Scholar
Fujimagari, T. (1980). On the extinction time distribution of a branching process in varying environments. Adv. Appl. Prob. 12, 350–366.CrossRefGoogle Scholar
Haccou, P., Jagers, P. and Vatutin, V. A. (2005). Branching Processes: Variation, Growth, and Extinction of Populations. Cambridge University Press.CrossRefGoogle Scholar
Jagers, P. (1974). Galton–Watson processes in varying environment. J. Appl. Prob. 11, 174–178.CrossRefGoogle Scholar
James, N., Lyons, R. and Peres, Y. (2008). A transient Markov chain with finitely many cutpoints. In Probability and Statistics: Essays in Honor of David A. Freedman (IMS Collections 2), eds D. Nolan and T. Speed. Institute of Mathematical Statistics, pp. 24–29.CrossRefGoogle Scholar
Jones, O. D. (1997). On the convergence of multitype branching processes with varying environments. Ann. Appl. Prob. 7, 772–801.CrossRefGoogle Scholar
Kersting, G. (2020). A unifying approach to branching processes in a varying environment. J. Appl. Prob. 57, 196–220.CrossRefGoogle Scholar
Kersting, G. and Vatutin, V. (2017). Discrete Time Branching Processes in Random Environment. John Wiley, New York.CrossRefGoogle Scholar
Kesten, H., Kozlov, M. V. and Spitzer, F. (1975). A limit law for random walk in a random environment. Compositio Math. 30, 145–168.Google Scholar
Key, E. S. (1987). Limiting distributions and regeneration times for multitype branching processes with immigration in a random environment. Ann. Prob. 15, 344–353.CrossRefGoogle Scholar
Kimmel, M. and Axelrod, D. E. (2015). Branching Processes in Biology. Springer, New York.CrossRefGoogle Scholar
Lindvall, T. (1974). Almost sure convergence of branching processes in varying and random environments. Ann. Prob. 2, 344–346.CrossRefGoogle Scholar
Lorentzen, L. (1995). Computation of limit periodic continued fractions. A survey. Numer. Algorithms 10, 69–111.CrossRefGoogle Scholar
Macphee, I. M. and Schuh, H. J. (1983). A Galton–Watson branching process in varying environments with essentially constant means and two rates of growth. Austrl. N. Z. J. Statist. 25, 329–338.CrossRefGoogle Scholar
Petrov, V. V. (2004). A generalization of the Borel–Cantelli lemma. Statist. Prob. Lett. 67, 233–239.CrossRefGoogle Scholar
Roitershtein, A. (2007). A note on multitype branching processes with immigration in a random environment. Ann. Prob. 35, 1573–1592.CrossRefGoogle Scholar
Sigman, K. and Wolff, R. W. (1993). A review of regenerative process. SIAM Rev. 35, 269–288.CrossRefGoogle Scholar
Wang, H. M. (2013). A note on multitype branching process with bounded immigration in random environment. Acta Math. Sin. (Engl. Ser.) 29, 1095–1110.CrossRefGoogle Scholar
Wang, H. M. (2019). On the number of points skipped by a transient (1,2) random walk on the lattice of the positive half line. Markov Process. Relat. Fields 25, 125–148.Google Scholar
Wang, H. M. (2021). On extinction time distribution of a 2-type linear-fractional branching process in a varying environment with asymptotically constant mean matrices. Preprint, arXiv:2106.01203 [math.PR].Google Scholar
Wang, H. M. (2021). Asymptotics of entries of products of nonnegative 2-by-2 matrices. Preprint, arXiv:2111.10232 [math.PR].Google Scholar
Wang, H. M. and Yao, H. (2022). Two-type linear fractional branching processes in varying environments with asymptotically constant mean matrices. J. Appl. Prob. 59, 224–255.CrossRefGoogle Scholar