Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Balmer, D. W.
1972.
A single server queue in discrete time with customers served in random order.
Journal of Applied Probability,
Vol. 9,
Issue. 4,
p.
862.


 be the family of all functions from the positive integers into the positive integers, which satisfy
be the family of all functions from the positive integers into the positive integers, which satisfy

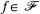 are random functions with probabilities
are random functions with probabilities