Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T15:57:23.832Z Has data issue: false hasContentIssue false
  • English
  • Français

On the rate of convergence for extremes of mean square differentiable stationary normal processes

Part of: Limit theorems Stochastic processes

Published online by Cambridge University Press:  14 July 2016

Marie F. Kratz  and
Holger Rootzén
Marie F. Kratz*
Affiliation:
Université René Descartes
Holger Rootzén*
Affiliation:
Chalmers University of Technology
*
∗Postal address: UFR de Mathématiques et Informatique, Université René Descartes, Paris V, 45 rue des Saints-Pères, 75270 Paris Cedex 06, France. e-mail: [email protected]
∗∗Postal address: Department of Mathematics, Chalmers University of Technology, S-41962 Göteborg, Sweden. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let ξ (t); t ≧ 0 be a normalized continuous mean square differentiable stationary normal process with covariance function r(t). Further, let 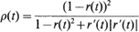and set 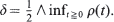. We give bounds which are roughly of order Τ –δ for the rate of convergence of the distribution of the maximum and of the number of upcrossings of a high level by ξ (t) in the interval [0, T]. The results assume that r(t) and r′(t) decay polynomially at infinity and that r″ (t) is suitably bounded. For the number of upcrossings it is in addition assumed that r(t) is non-negative.

Keywords

RATE OF CONVERGENCEEXTREMESNORMAL PROCESSESPOISSON CONVERGENCE

MSC classification

Primary: 60G70: Extreme value theory; extremal processes
Secondary: 60G15: Gaussian processes 60F05: Central limit and other weak theorems
Type
Research Papers
Information
Journal of Applied Probability , Volume 34 , Issue 4 , December 1997 , pp. 908 - 923
Copyright
Copyright © Applied Probability Trust 1997 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barbour, A. D., Holst, L. and Janson, S. (1992) Poisson Approximation. Oxford Science Publishers, Oxford.CrossRefGoogle Scholar
Berman, S. M. (1971) Excursions above high levels for stationary Gaussian processes. Pacific J. Math. 36, 63–79.CrossRefGoogle Scholar
Cramér, H. (1965) A limit theorem for the maximum values of certain stochastic processes. Theory Prob. Appl. 10, 126–128.CrossRefGoogle Scholar
Cramer, H. and Leadbetter, M. R. (1967) Stationary and Related Stochastic Processes. Wiley, New York.Google Scholar
Falk, M., Hüsler, J. and Reiss, R. D. (1994) Laws of Small Numbers: Extremes and Rare Events. Birkhaüser, Basel.Google Scholar
Holst, L. and Janson, S. (1990) Poisson approximation using the Stein-Chen method and coupling: number of exceedances of Gaussian random variables. Ann. Prob. 18, 713–723.CrossRefGoogle Scholar
Leadbetter, M. R., Lindgren, G. and Rootzén, H. (1978) Conditions for the convergence in distribution of maxima of stationary normal processes. Stoch. Proc. Appl. 8, 131–139.CrossRefGoogle Scholar
Leadbetter, M. R., Lindgren, G. and Rootzén, H. (1983) Extremes and Related Properties of Random Sequences and Processes. Springer, New York.CrossRefGoogle Scholar
Pickersgill, E. A. and Piterbarg, V. I. (1987) Estimation of the rate of convergence in a Poisson limit theorem for the excursions of stationary Gaussian processes. Theory Prob. Math. Statist. 36 (in Russian).Google Scholar
Pickands, J. III (1969) Upcrossing probabilities for stationary Gaussian processes. Trans. Amer. Math. Soc. 145, 51–73.CrossRefGoogle Scholar
Piterbarg, V. I. (1982) Large deviations of random processes close to Gaussian ones. Theory Prob. Appl. 27, 504–524.CrossRefGoogle Scholar
Rootzen, H. (1983) The rate of convergence of extremes of stationary normal sequences. Adv. Appl. Prob. 15, 54–80.CrossRefGoogle Scholar
Volkonskii, V. A. and Rozanov, Yu. A. (1961) Some limit theorems for random functions II. Theory Prob. Appl. 6, 186–198.CrossRefGoogle Scholar