Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T14:03:06.888Z Has data issue: false hasContentIssue false
  • English
  • Français

On the prediction of fractional Brownian motion

Part of: Stochastic processes

Published online by Cambridge University Press:  14 July 2016

Gustaf Gripenberg  and
Ilkka Norros
Gustaf Gripenberg*
Affiliation:
University of Helsinki
Ilkka Norros*
Affiliation:
VTT Information Technology
*
∗Postal address: University of Helsinki, Department of Mathematics, P.O. Box 4, 00014 University of Helsinki, Finland. e-mail:[email protected]
∗∗Postal address: VTT Information Technology, Telecommunications, P.O. Box 1202, 02044 VTT, Finland. e-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

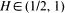Integration with respect to the fractional Brownian motion Z with Hurst parameter is discussed. The predictor 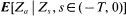is represented as an integral with respect to Z, solving a weakly singular integral equation for the prediction weight function.

Keywords

FRACTIONAL BROWNIAN MOTIONPREDICTIONSTOCHASTIC INTEGRATION

MSC classification

Primary: 60G25: Prediction theory
Secondary: 60G15: Gaussian processes 60G18: Self-similar processes
Type
Research Papers
Information
Journal of Applied Probability , Volume 33 , Issue 2 , September 1996 , pp. 400 - 410
Copyright
Copyright © Applied Probability Trust 1996 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Abramowitz, M. A. and Stegun, I. A. (1970) Handbook of Mathematical Functions. Dover, New York.Google Scholar
[2] Cornfeld, I. P., Sinai, Ya. G. and Fomin, S. V. (1982) Ergodic Theory. Springer, Berlin.CrossRefGoogle Scholar
[3] Dellacherie, C. and Meyer, P.-A. (1982) Probabilities and Potential. North Holland, Amsterdam.Google Scholar
[4] Eberlein, E. and Taqqu, M. S. (1986) Dependence in Probability and Statistics. (Prog. Prob. Stat. Vol. 11). Birkhäuser, Boston.Google Scholar
[5] Fowler, H. J. and Leland, W. E. (1991) Local area network traffic characteristics, with implications for broadband network congestion management. IEEE J. Sel. Areas Commun. 9, 1139–1149.Google Scholar
[6] Huang, S. T. and Cambanis, S. (1978) Stochastic and multiple Wiener integrals for Gaussian processes. Ann. Prob. 6, 585–614.CrossRefGoogle Scholar
[7] Leland, W. E., Taqqu, M. S., Willinger, W. and Wilson, D. V. (1994) On the self-similar nature of Ethernet traffic (extended version). IEEE/ACM Trans. Networking 2, 1–15.Google Scholar
[8] Lundgren, T. and Chiang, D. (1967) Solution of a class of singular integral equations. Quart. J. Appl. Math. 24, 303–313.CrossRefGoogle Scholar
[9] Mandelbrot, B. B. and Van Ness, J. W. (1968) Fractional Brownian motions, fractional noises and applications. SIAM Rev. 10, 422–437.Google Scholar
[10] Norros, I. (1994) A storage model with self-similar input. Queueing Systems 16, 387–396.Google Scholar