Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-19T23:54:21.461Z Has data issue: false hasContentIssue false
  • English
  • Français

On the existence of quasi-stationary distributions in denumerable R-transient Markov chains

Part of: Markov processes Limit theorems

Published online by Cambridge University Press:  14 July 2016

Masaaki Kijima
Masaaki Kijima*
Affiliation:
The University of Tsukuba, Tokyo
*
∗ Postal address: Graduate School of Systems Management, The University of Tsukuba, Tokyo, 3–29–1 Otsuka, Bunkyo-ku, Tokyo 112, Japan.
Get access Rights & Permissions [Opens in a new window]

Abstract

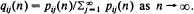Let {Xn, n = 0, 1, 2, ···} be a transient Markov chain which, when restricted to the state space 𝒩 + = {1, 2, ···}, is governed by an irreducible, aperiodic and strictly substochastic matrix 𝐏 = (pij), and let pij(n) = P ∈ Xn = j, Xk ∈ 𝒩+ for k = 0, 1, ···, n | X0 = i], i, j 𝒩 +. The prime concern of this paper is conditions for the existence of the limits, qij say, of as n →∞. If 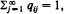the distribution (qij) is called the quasi-stationary distribution of {Xn} and has considerable practical importance. It will be shown that, under some conditions, if a non-negative non-trivial vector x = (xi) satisfying rxT = xT𝐏 and 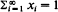exists, where r is the convergence norm of 𝐏, i.e. r = R–1 and 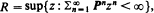and T denotes transpose, then it is unique, positive elementwise, and qij(n) necessarily converge to xj as n →∞. Unlike existing results in the literature, our results can be applied even to the R-null and R-transient cases. Finally, an application to a left-continuous random walk whose governing substochastic matrix is R-transient is discussed to demonstrate the usefulness of our results.

Keywords

SUBSTOCHASTIC MATRIXCONVERGENCE NORMLEFT INVARIANT VECTORCONDITIONAL TRANSITION PROBABILITYRATIO LIMIT THEOREMLEFT-CONTINUOUS RANDOM WALK

MSC classification

Primary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Secondary: 60F99: None of the above, but in this section
Type
Research Papers
Information
Journal of Applied Probability , Volume 29 , Issue 1 , March 1992 , pp. 21 - 36
Copyright
Copyright © Applied Probability Trust 1992 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Blackwell, D. (1955) On transient Markov process with a countable number of states and stationary transition probabilities. Ann. Math. Statist. 26, 654–658.Google Scholar
[2]Chung, K. L. (1960) Markov Chains with Stationary Transition Probabilities. Springer-Verlag, Berlin.Google Scholar
[3]Daley, D. J. (1969) Quasi-stationary behaviour of a left-continuous random walk. Ann. Math. Statist. 40, 532–539.Google Scholar
[4]Darroch, J. N. and Seneta, E. (1967) On quasi-stationary distributions in absorbing continuous-time finite Markov chains. J. Appl. Prob. 4, 192–196.Google Scholar
[5]Freedman, D. (1983) Markov Chains. Springer-Verlag, New York.Google Scholar
[6]Harris, T. E. (1957) Transient Markov chains with stationary measures. Proc. Amer. Math. Soc. 8, 937–942.Google Scholar
[7]Iglehart, D. L. (1974) Random walks with negative drift conditioned to stay positive. J. Appl. Prob. 11, 742–751.Google Scholar
[8]Karlin, S. and Mcgregor, J. (1959) Random walks. Illinois J. Math. 3, 66–81.Google Scholar
[9]Kijima, M. (1987) Some results for uniformizable semi-Markov processes. Austral. J. Statist. 29, 193–207.Google Scholar
[10]Kijima, M. (1989) On the relaxation time for single server queues. J. Operat. Res. Soc. Japan 32, 103–111.Google Scholar
[11]Kijima, M. (1991) Quasi-stationary distributions of phase-type queues. Math. Operat. Res. To appear.Google Scholar
[12]Kijima, M. and Seneta, E. (1991) Some results for quasi-stationary distributions of birth-death processes. J. Appl. Prob. 28, 503–511.Google Scholar
[13]Kyprianou, E. K. (1971) On the quasi-stationary distribution of the virtual waiting time in queues with Poisson arrivals. J. Appl. Prob. 8, 494–507.Google Scholar
[14]Pakes, A. G. and Pollett, P. K. (1989) The supercritical birth, death and catastrophe process: limit theorems on the set of extinction. Stoch. Proc. Appl. 32, 161–170.Google Scholar
[15]Pollett, P. K. and Roberts, A. J. (1990) A description of the long-term behavior of absorbing continuous-time Markov chains using a centre manifold. Adv. Appl. Prob. 22, 111–128.Google Scholar
[16]Pruitt, W. E. (1964) Eigenvalues of non-negative matrices. Ann. Math. Statist. 35, 1797–1800.Google Scholar
[17]Seneta, E. (1981) Non-Negative Matrices and Markov Chains, 2nd edn. Springer-Verlag, New York.Google Scholar
[18]Seneta, E. and Vere-Jones, D. (1966) On quasi-stationary distributions in discrete-time Markov chains with a denumerable infinity of states. J. Appl. Prob. 3, 403–434.Google Scholar
[19]Van Doorn, E. A. (1991) Quasi-stationary distributions and convergence to quasi-stationarity of birth-death processes. Adv. Appl. Prob. 23, 683–700.Google Scholar
[20]Veech, W. (1963) The necessity of Harris's condition for the existence of a stationary measure. Proc. Amer. Math. Soc. 14, 856–860.Google Scholar
[21]Vere-Jones, D. (1962) Geometric ergodicity in denumerable Markov chains. Quart. J. Math. Oxford 13, 7–28.Google Scholar