Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Barabás, Béla
Csörgő, Miklós
Horváth, Lajos
and
Yandell, Brian S.
1986.
Bootstrapped confidence bands for percentile lifetime.
Annals of the Institute of Statistical Mathematics,
Vol. 38,
Issue. 3,
p.
429.
Mustafi, C.K.
1987.
Residual median for non-identically distributed random variables.
Journal of Statistical Planning and Inference,
Vol. 17,
Issue. ,
p.
389.
1988.
Extreme Value Theory in Engineering.
p.
341.
Chung, Chang-Jo F
1989.
Confidence bands for percentile residual lifetime under random censorship model.
Journal of Multivariate Analysis,
Vol. 29,
Issue. 1,
p.
94.
Feng, Z.
and
Kulasekera, K.B.
1991.
Nonparametric estimation of the percentile residual life function.
Communications in Statistics - Theory and Methods,
Vol. 20,
Issue. 1,
p.
87.
Ruiz, J.M.
and
Navarro, J.
1994.
Characterization of distributions by relationships between failure rate and mean residual life.
IEEE Transactions on Reliability,
Vol. 43,
Issue. 4,
p.
640.
Gelfand, Alan E.
and
Kottas, Athanasios
2003.
Bayesian Semiparametric Regression for Median Residual Life.
Scandinavian Journal of Statistics,
Vol. 30,
Issue. 4,
p.
651.
Lillo, Rosa E.
2005.
On the median residual lifetime and its aging properties: A characterization theorem and applications.
Naval Research Logistics (NRL),
Vol. 52,
Issue. 4,
p.
370.
Jeong, Jong‐Hyeon
Jung, Sin‐Ho
and
Costantino, Joseph P.
2008.
Nonparametric Inference on Median Residual Life Function.
Biometrics,
Vol. 64,
Issue. 1,
p.
157.
Nair, N. Unnikrishnan
and
Sankaran, P. G.
2009.
Quantile-Based Reliability Analysis.
Communications in Statistics - Theory and Methods,
Vol. 38,
Issue. 2,
p.
222.
Jung, Sin‐Ho
Jeong, Jong‐Hyeon
and
Bandos, Hanna
2009.
Regression on Quantile Residual Life.
Biometrics,
Vol. 65,
Issue. 4,
p.
1203.
Ma, Yanyuan
and
Yin, Guosheng
2010.
Semiparametric median residual life model and inference.
Canadian Journal of Statistics,
Vol. 38,
Issue. 4,
p.
665.
Franco-Pereira, Alba M.
Lillo, Rosa E.
Romo, Juan
and
Shaked, Moshe
2011.
Percentile residual life orders.
Applied Stochastic Models in Business and Industry,
Vol. 27,
Issue. 3,
p.
235.
Unnikrishnan Nair, N.
and
Vineshkumar, B.
2011.
Reversed percentile residual life and related concepts.
Journal of the Korean Statistical Society,
Vol. 40,
Issue. 1,
p.
85.
Franco-Pereira, Alba M.
Lillo, Rosa E.
and
Romo, Juan
2011.
The percentile residual life up to time t0: Ordering and aging properties.
Journal of Statistical Planning and Inference,
Vol. 141,
Issue. 11,
p.
3554.
Franco-Pereira, Alba M.
Lillo, Rosa E.
and
Romo, Juan
2012.
Comparing quantile residual life functions by confidence bands.
Lifetime Data Analysis,
Vol. 18,
Issue. 2,
p.
195.
Franco-Pereira, Alba M.
Lillo, Rosa E.
and
Shaked, Moshe
2012.
The decreasing percentile residual life ageing notion.
Statistics,
Vol. 46,
Issue. 5,
p.
587.
Jeong, Jong‐Hyeon
and
Fine, Jason P.
2013.
Nonparametric inference on cause‐specific quantile residual life.
Biometrical Journal,
Vol. 55,
Issue. 1,
p.
68.
Franco‐Pereira, Alba M.
and
de Uña‐Álvarez, Jacobo
2013.
Estimation of a monotone percentile residual life function under random censorship.
Biometrical Journal,
Vol. 55,
Issue. 1,
p.
52.
Nair, N. Unnikrishnan
Sankaran, P. G.
and
Balakrishnan, N.
2013.
Quantile-Based Reliability Analysis.
p.
29.
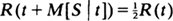 , where R is the reliability function. We actually study a more general functional equation f(φ(t)) = sf(t) called Schroder's equation. It is shown that, under mild assumptions on φ, the solution is of the form f(t) = f0(t)k(log f0 (t)), where f0 is a well-behaved particular solution which can be constructed and k is a periodic function; thus the solution is not unique. Two examples are solved to illustrate the method. Finally, these examples are used to solve the problem of linear M[S | t] studied by Schmittlein and Morrison. As an extra benefit, all of our results hold equally well for the more general sth percentile residual life function.
, where R is the reliability function. We actually study a more general functional equation f(φ(t)) = sf(t) called Schroder's equation. It is shown that, under mild assumptions on φ, the solution is of the form f(t) = f0(t)k(log f0 (t)), where f0 is a well-behaved particular solution which can be constructed and k is a periodic function; thus the solution is not unique. Two examples are solved to illustrate the method. Finally, these examples are used to solve the problem of linear M[S | t] studied by Schmittlein and Morrison. As an extra benefit, all of our results hold equally well for the more general sth percentile residual life function.

