Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-19T07:12:28.595Z Has data issue: false hasContentIssue false
  • English
  • Français

On the classical Bonferroni inequalities and the corresponding Galambos inequalities

Published online by Cambridge University Press:  14 July 2016

A. M. Walker
A. M. Walker*
Affiliation:
University of Sheffield
*
∗Postal address: Department of Probability and Statistics, The University, Sheffield S3 7RH, U.K.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let (A1A2, · ··, An) be a set of n events on a probability space. Let 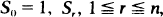be the sum of the probabilities of all 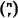intersections of r events, and Mn the number of events in the set which occur. The classical Bonferroni inequalities provide upper and lower bounds for the probabilities P(Mn = m), 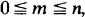and 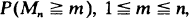equal to partial sums of series of the form 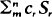which give the exact probabilities. These inequalities have recently been extended by J. Galambos to give sharper bounds.

Here we present straightforward proofs of the Bonferroni inequalities, using indicator functions, and show how they lead naturally to new simple proofs of the Galambos inequalities.

Keywords

EVENTSNUMBER OF OCCURRENCESBONFERRONI INEQUALITIESGALAMBOS INEQUALITIESINDICATOR FUNCTION METHOD
Type
Short Communications
Information
Journal of Applied Probability , Volume 18 , Issue 3 , September 1981 , pp. 757 - 763
Copyright
Copyright © Applied Probability Trust 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Feller, W. (1968) An Introduction to Probability Theory and its Applications, Vol. 1, 3rd edn. Wiley, New York.Google Scholar
Galambos, J. (1977) Bonferroni inequalities. Ann. Prob. 5, 577–581.Google Scholar
Galambos, J. (1978) The Asymptotic Theory of Extreme Order Statistics. Wiley, New York.Google Scholar
Loève, M. (1942) Sur les systèmes d'évènements. Ann. Univ. Lyon, Sect. A 5, 55–74.Google Scholar
Moran, P. A. P. (1968) An Introduction to Probability Theory. Clarendon Press, Oxford.Google Scholar
Parzen, E. (1960) Modern Probability Theory and Its Applications. Wiley, New York.CrossRefGoogle Scholar