Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-09T12:18:39.619Z Has data issue: false hasContentIssue false
  • English
  • Français

On Fibonacci (or lagged Bienaymé-Galton-Watson) branching processes

Published online by Cambridge University Press:  14 July 2016

C. C. Heyde
C. C. Heyde*
Affiliation:
CSIRO Division of Mathematics and Statistics, Canberra
*
∗Postal address: CSIRO Division of Mathematics and Statistics, P.O. Box 1965 Canberra City, ACT 2601, Australia.
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is concerned with a discrete-time population model in which a new individual entering the population at time t can produce offspring for the first time at time t + 2 and then subsequently at times t + 3, t + 4, ···. The numbers of offspring produced on each occasion are independent random variables each with the distribution of Z for which EZ = m <∞, and individuals have independent lines of descent. This model is contrasted with the corresponding Bienaymé-Galton-Watson one. If Xn denotes the number of individuals in the population at time n, it is shown that z–nXn almost surely converges to a random variable W, as n→∞, where 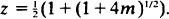Various properties of W are obtained, in particular W > 0 a.s. if and only if EZ | log Z | < ∞ Results are also given on the rate of convergence of 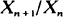to z when Var Z < ∞ and these display a surprising dependence on the size of z.

Keywords

BRANCHING PROCESSESPOPULATION PROCESSESGALTON-WATSON PROCESSESGROWTH RATESESTIMATIONFIBONACCI NUMBERS
Type
Research Papers
Information
Journal of Applied Probability , Volume 18 , Issue 3 , September 1981 , pp. 583 - 591
Copyright
Copyright © Applied Probability Trust 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Billingsley, P. (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
Doney, R. A. (1972) A limit theorem for a class of supercritical branching processes. J. Appl. Prob. 9, 707–724.CrossRefGoogle Scholar
Heyde, C. C. (1980) On a probabilistic analogue of the Fibonacci sequence. J. Appl. Prob. 17, 1079–1082.CrossRefGoogle Scholar
Jagers, P. (1975) Branching Processes with Biological Applications. Wiley, London.Google Scholar
Nerman, O. (1980) On the convergence of supercritical general (C-M-J) branching processes I, II. Z. Wahrscheinlichkeitsth. Google Scholar
Scott, D. J. (1978) A central limit theorem for martingales and an application to branching processes. Stoch. Proc. Appl. 6, 241–252.CrossRefGoogle Scholar