Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Taniguchi, Masanobu
1981.
An Estimation Procedure of Parameters of a Certain Spectral Density Model.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 43,
Issue. 1,
p.
34.
Linhart, H.
and
Volkers, P.
1985.
On a criterion for the selection of models for stationary time series.
Metrika,
Vol. 32,
Issue. 1,
p.
181.
Bhansali, R. J.
1986.
THE CRITERION AUTOREGRESSIVE TRANSFER FUNCTION OF PARZEN.
Journal of Time Series Analysis,
Vol. 7,
Issue. 2,
p.
79.
Hurvich, Clifford M.
Simonoff, Jeffrey S.
and
Zeger, Scott L.
1991.
VARIANCE ESTIMATION FOR SAMPLE AUTOCOVARIANCES: DIRECT AND RESAMPLING APPROACHES.
Australian Journal of Statistics,
Vol. 33,
Issue. 1,
p.
23.
Sesay, S. A. O.
and
Rao, T. Subba
1992.
FREQUENCY‐DOMAIN ESTIMATION OF BILINEAR TIME SERIES MODELS.
Journal of Time Series Analysis,
Vol. 13,
Issue. 6,
p.
521.
von Sachs, R.
1993.
Estimating the Spectrum of a Stochastic Process in the Presence of a Contaminating Signal.
IEEE Transactions on Signal Processing,
Vol. 41,
Issue. 1,
p.
323.
Taniguchi, Masanobu
and
Kondo, Masao
1993.
NON‐PARAMETRIC APPROACH IN TIME SERIES ANALYSIS.
Journal of Time Series Analysis,
Vol. 14,
Issue. 4,
p.
397.
Sachs, Rainer von
1994.
PEAK‐INSENSITIVE NON‐PARAMETRIC SPECTRUM ESTIMATION.
Journal of Time Series Analysis,
Vol. 15,
Issue. 4,
p.
429.
Janas, Daniel
and
Sachs, Rainer von
1995.
CONSISTENCY FOR NON‐LINEAR FUNCTIONS OF THE PERIODOGRAM OF TAPERED DATA.
Journal of Time Series Analysis,
Vol. 16,
Issue. 6,
p.
585.
Mohanty, R.
and
Pourahmadi, M.
1996.
Estimation of the Generalized Prediction Error Variance of a Multiple Time Series.
Journal of the American Statistical Association,
Vol. 91,
Issue. 433,
p.
294.
Li, Lei
and
Xie, Zhongjie
1996.
MODEL SELECTION AND ORDER DETERMINATION FOR TIME SERIES BY INFORMATION BETWEEN THE PAST AND THE FUTURE.
Journal of Time Series Analysis,
Vol. 17,
Issue. 1,
p.
65.
Benn, A.G.
and
Kulperger, R.J.
1997.
Integrated marked Poisson processes with application to image correlation spectroscopy.
Canadian Journal of Statistics,
Vol. 25,
Issue. 2,
p.
215.
Deo, Rohit S.
and
Chen, Willa W.
2000.
On the integral of the squared periodogram.
Stochastic Processes and their Applications,
Vol. 85,
Issue. 1,
p.
159.
Drouiche, K.
2000.
A new test for whiteness.
IEEE Transactions on Signal Processing,
Vol. 48,
Issue. 7,
p.
1864.
Fay, Gilles
and
Philippe, Anne
2002.
Goodness-of-fit test for long range dependent processes.
ESAIM: Probability and Statistics,
Vol. 6,
Issue. ,
p.
239.
Stoica, Petre
and
Sandgren, Niclas
2006.
Smoothed nonparametric spectral estimation via cepsturm thresholding - Introduction of a method for smoothed nonparametric spectral estimation.
IEEE Signal Processing Magazine,
Vol. 23,
Issue. 6,
p.
34.
2007.
Optimal Statistical Inference in Financial Engineering.
p.
355.
Stoica, Petre
and
Sandgren, Niclas
2007.
Total-Variance Reduction Via Thresholding: Application to Cepstral Analysis.
IEEE Transactions on Signal Processing,
Vol. 55,
Issue. 1,
p.
66.
Reddy, T Sreenivasulu
and
Ramachandra Reddy, G
2010.
MST Radar Signal Processing Using Cepstral Thresholding.
IEEE Transactions on Geoscience and Remote Sensing,
Vol. 48,
Issue. 6,
p.
2704.
Faÿ, Gilles
2010.
Moment bounds for non-linear functionals of the periodogram.
Stochastic Processes and their Applications,
Vol. 120,
Issue. 6,
p.
983.


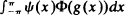 whose asymptotic variance is
whose asymptotic variance is 