Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Taniguchi, Masanobu
1980.
On estimation of the integrals of certain functions of spectral density.
Journal of Applied Probability,
Vol. 17,
Issue. 01,
p.
73.
Taniguchi, Masanobu
1980.
On selection of the order of the spectral density model for a stationary process.
Annals of the Institute of Statistical Mathematics,
Vol. 32,
Issue. 3,
p.
401.
Taniguchi, Masanobu
1981.
An Estimation Procedure of Parameters of a Certain Spectral Density Model.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 43,
Issue. 1,
p.
34.
Bhansali, R. J.
1986.
THE CRITERION AUTOREGRESSIVE TRANSFER FUNCTION OF PARZEN.
Journal of Time Series Analysis,
Vol. 7,
Issue. 2,
p.
79.
Taniguchi, Masanobu
1987.
Minimum Contrast Estimation for Spectral Densities of Stationary Processes.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 49,
Issue. 3,
p.
315.
Sesay, S. A. O.
and
Rao, T. Subba
1992.
FREQUENCY‐DOMAIN ESTIMATION OF BILINEAR TIME SERIES MODELS.
Journal of Time Series Analysis,
Vol. 13,
Issue. 6,
p.
521.
Yajima, Yoshihiro
1993.
New Directions in Time Series Analysis.
Vol. 46,
Issue. ,
p.
375.
Dahlhaus, R.
and
Wefelmeyer, W.
1996.
Asymptotically optimal estimation in misspecified time series models.
The Annals of Statistics,
Vol. 24,
Issue. 3,
Lang, Gabriel
and
Azaı̈s, Jean-Marc
1999.
Non-parametric estimation of the long-range dependence exponent for Gaussian processes.
Journal of Statistical Planning and Inference,
Vol. 80,
Issue. 1-2,
p.
59.
FAY, GILLES
MOULINES, ERIC
and
SOULIER, PHILIPPE
2002.
Nonlinear functionals of the periodogram.
Journal of Time Series Analysis,
Vol. 23,
Issue. 5,
p.
523.
Taniguchi, Masanobu
van Garderen, Kees Jan
and
Puri, Madan L.
2003.
HIGHER ORDER ASYMPTOTIC THEORY FOR MINIMUM CONTRAST ESTIMATORS OF SPECTRAL PARAMETERS OF STATIONARY PROCESSES.
Econometric Theory,
Vol. 19,
Issue. 06,
Dette, Holger
and
Spreckelsen, Ingrid
2003.
A Note on a Specification Test for Time Series Models Based on Spectral Density Estimation.
Scandinavian Journal of Statistics,
Vol. 30,
Issue. 3,
p.
481.
Chen, Willa W.
and
Deo, Rohit S.
2006.
Estimation of mis-specified long memory models.
Journal of Econometrics,
Vol. 134,
Issue. 1,
p.
257.
Stoica, Petre
and
Sandgren, Niclas
2006.
Cepstrum Thresholding Scheme for Nonparametric Estimation of Smooth Spectra.
p.
874.
Stoica, Petre
and
Sandgren, Niclas
2006.
Smoothed nonparametric spectral estimation via cepsturm thresholding - Introduction of a method for smoothed nonparametric spectral estimation.
IEEE Signal Processing Magazine,
Vol. 23,
Issue. 6,
p.
34.
Sandgren, N.
and
Stoica, P.
2006.
On Nonparametric Estimation of 2-D Smooth Spectra.
IEEE Signal Processing Letters,
Vol. 13,
Issue. 10,
p.
632.
Faÿ, Gilles
2010.
Moment bounds for non-linear functionals of the periodogram.
Stochastic Processes and their Applications,
Vol. 120,
Issue. 6,
p.
983.
Leonenko, Ganna
Los, Sietse
and
North, Peter
2013.
Statistical Distances and Their Applications to Biophysical Parameter Estimation: Information Measures, M-Estimates, and Minimum Contrast Methods.
Remote Sensing,
Vol. 5,
Issue. 3,
p.
1355.
Leonenko, G.
Los, S.O.
and
North, P.R.J.
2013.
Retrieval of leaf area index from MODIS surface reflectance by model inversion using different minimization criteria.
Remote Sensing of Environment,
Vol. 139,
Issue. ,
p.
257.
Rivera, Juan
Verrelst, Jochem
Leonenko, Ganna
and
Moreno, José
2013.
Multiple Cost Functions and Regularization Options for Improved Retrieval of Leaf Chlorophyll Content and LAI through Inversion of the PROSAIL Model.
Remote Sensing,
Vol. 5,
Issue. 7,
p.
3280.


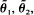 by minimizing two criteria
by minimizing two criteria 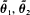 with respect to efficiency and robustness.
with respect to efficiency and robustness.