Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Asmussen, Søren
1982.
On The Role of a Certain Eigenvalue in Estimating the Growth Rate of a Branching Process.
Australian Journal of Statistics,
Vol. 24,
Issue. 2,
p.
151.
Dawson, R.
Gabor, G.
Nowakowski, R.
and
Wiens, D.
1985.
Random Fibonacci-Type Sequences.
The Fibonacci Quarterly,
Vol. 23,
Issue. 2,
p.
169.
Asmussen, Søren
1986.
Semi-Markov Models.
p.
385.
Shannon, A.G.
Clarke, J.H.
and
Hills, L.J.
1987.
Contingency relations for infectious diseases.
Computers & Mathematics with Applications,
Vol. 14,
Issue. 9-12,
p.
829.
Barabé, Denis
2006.
Stochastic approaches in phyllotaxis.
Canadian Journal of Botany,
Vol. 84,
Issue. 11,
p.
1675.
Stoica, George
and
Li, Deli
2009.
Expected gains in the MacQueen–Heyde model.
Statistics & Probability Letters,
Vol. 79,
Issue. 14,
p.
1634.
Liptai, Kálmán
and
Szalay, László
2024.
Distribution Generated by a Random Inhomogenous Fibonacci Sequence.
Mediterranean Journal of Mathematics,
Vol. 21,
Issue. 1,


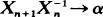 a.s. as
a.s. as