Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-05T02:07:04.015Z Has data issue: false hasContentIssue false
  • English
  • Français

On a class of random walks in simplexes

Part of: Markov processes Limit theorems

Published online by Cambridge University Press:  16 July 2020

Tuan-Minh Nguyen  and
Stanislav Volkov
Tuan-Minh Nguyen*
Affiliation:
Monash University
Stanislav Volkov*
Affiliation:
Lund University
*
*Postal address: School of Mathematical Sciences, Monash University, Victoria 3800, Australia
**Postal address: Centre for Mathematical Sciences, Lund University, Lund 22100-118, Sweden
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the limit behaviour of a class of random walk models taking values in the standard d-dimensional (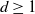 $d\ge 1$ ) simplex. From an interior point z, the process chooses one of the 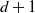$d+1$ vertices of the simplex, with probabilities depending on z, and then the particle randomly jumps to a new location z′ on the segment connecting z to the chosen vertex. In some special cases, using properties of the Beta distribution, we prove that the limiting distributions of the Markov chain are Dirichlet. We also consider a related history-dependent random walk model in [0, 1] based on an urn-type scheme. We show that this random walk converges in distribution to an arcsine random variable.

Keywords

Random walks in simplexesiterated random functionsDirichlet distributionstick-breaking process

MSC classification

Primary: 60J05: Discrete-time Markov processes on general state spaces
Secondary: 60F05: Central limit and other weak theorems
Type
Research Papers
Information
Journal of Applied Probability , Volume 57 , Issue 2 , June 2020 , pp. 409 - 428
Copyright
© Applied Probability Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Borovkov, A. A. (1998). Ergodicity and Stability of Stochastic Processes. Wiley, New York.Google Scholar
DeGroot, M. H. and Rao, M. M. (1963). Stochastic give-and-take. J. Math. Anal. Appl. 7, 489–498.10.1016/0022-247X(63)90071-4CrossRefGoogle Scholar
Diaconis, P. and Freedman, D. (1999). Iterated random functions. SIAM Rev. 41 (1), 45–76.10.1137/S0036144598338446CrossRefGoogle Scholar
Hitczenko, P. and Letac, G. (2014). Dirichlet and quasi-Bernoulli laws for perpetuities. J. Appl. Prob. 51 (2), 400–416.10.1239/jap/1402578633CrossRefGoogle Scholar
Hofrichter, J., Jost, J., andTran, T. (2017). Information Geometry and Population Genetics: The Mathematical Structure of the Wright–Fisher Model. Springer, Cham.10.1007/978-3-319-52045-2CrossRefGoogle Scholar
Ladjimi, F.and Peigné, M. (2019). On the asymptotic behavior of the Diaconis–Freedman chain on [0, 1]. Statist. Prob. Lett. 145 (2), 1–11.10.1016/j.spl.2018.05.019CrossRefGoogle Scholar
McKinlay, S. and Borovkov, K. (2016). On explicit form of the stationary distributions for a class of bounded Markov chains. J. Appl. Prob. 53 (1), 231–243.10.1017/jpr.2015.21CrossRefGoogle Scholar
Pacheco-González, C. G. (2009). Ergodicity of a bounded Markov chain with attractiveness towards the centre. Statist. Prob. Lett. 79 (20), 2177–2181.10.1016/j.spl.2009.07.013CrossRefGoogle Scholar
Ramli, M. A. and Leng, G. (2010). The stationary probability density of a class of bounded Markov processes. Adv. Appl. Prob. 42 (4), 986–993.10.1239/aap/1293113147CrossRefGoogle Scholar
Sethuraman, J. (1994). A constructive definition of Dirichlet priors. Statist. Sinica 4 (2), 639–650.Google Scholar