Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T12:40:27.524Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on the expected number of survivors in supercritical carrier-borne epidemics

Published online by Cambridge University Press:  14 July 2016

Roy Saunders ,
Claude Lefèvre  and
Richard J. Kryscio
Roy Saunders*
Affiliation:
Northern Illinois University
Claude Lefèvre*
Affiliation:
Université Libre de Bruxelles
Richard J. Kryscio*
Affiliation:
Northern Illinois University
*
∗ Postal address: Department of Mathematical Sciences, Northern Illinois University, DeKalb, Illinois 60115, U.S.A. Research partially supported by National Science Foundation Grant No. MCS 77-03582.
∗∗ Postal address: Institut de Statistiques, Université Libre de Bruxelles, Campus Plaine C.P.210, Boulevard du Triomphe, B-1050 Bruxelles, Belgium.
∗ Postal address: Department of Mathematical Sciences, Northern Illinois University, DeKalb, Illinois 60115, U.S.A. Research partially supported by National Science Foundation Grant No. MCS 77-03582.
Get access Rights & Permissions [Opens in a new window]

Abstract

We provide a formal proof of a conclusion due to Abakuks (1974) which states that the expected number of survivors in Downton's carrier-borne epidemic model approaches the limit (ρ /π)δ as the initial number of susceptibles tends to infinity. Here ρ denotes the relative removal rate for carriers, π denotes the conditional probability that an infected susceptible will become a carrier, δ denotes the Kronecker delta function and 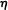denotes the initial number of carriers.

Keywords

CARRIER-BORNE EPIDEMICSEXPECTED NUMBER OF SURVIVORSSUPERCRITICAL
Type
Short Communications
Information
Journal of Applied Probability , Volume 16 , Issue 3 , September 1979 , pp. 646 - 650
Copyright
Copyright © Applied Probability Trust 1979 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abakuks, A. (1974) A note on supercritical carrier-borne epidemics. Biometrika 61, 271–275.Google Scholar
Daniels, H. E. (1972) An exact relation in the theory of carrier-borne epidemics. Biometrika 59, 211–213.Google Scholar
Downton, F. (1968) The ultimate size of carrier-borne epidemics. Biometrika 55, 277–289.Google Scholar
Feller, W. (1968) An Introduction to Probability Theory and its Applications, Vol. 1, 3rd edn. Wiley, New York.Google Scholar
Weiss, G. H. (1965) On the spread of epidemics by carriers. Biometrics 21, 481–490.Google Scholar