Objects of various integer sizes, o1, · ··, on, are to be packed together into bins of size N as they arrive at a service facility. The number of objects of size oi which arrive by time t is 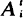, where the components of 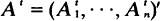are independent renewal processes, with At/t → λ as t → ∞. The empty space in those bins which are neither empty nor full at time t is called the wasted space and the system is declared stabilizable if for some finite B there exists a bin-packing algorithm whose use guarantees the expected wasted space is less than B for all t. We show that the system is stabilizable if the arrival processes are Poisson and λ lies in the interior of a certain convex polyhedral cone Λ. In this case there exists a bin-packing algorithm which stabilizes the system without needing to know λ. However, if λ lies on the boundary of Λ the wasted space grows as 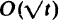and if λ is exterior to Λ it grows as O(t); these conclusions hold even if objects may be repacked as often as desired.