Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T05:52:52.980Z Has data issue: false hasContentIssue false
  • English
  • Français

Necessary and sufficient conditions for recurrence and transience of Markov chains, in terms of inequalities

Published online by Cambridge University Press:  14 July 2016

Jean-François Mertens ,
Ester Samuel-Cahn  and
Shmuel Zamir
Jean-François Mertens
Affiliation:
Université de Louvain
Ester Samuel-Cahn
Affiliation:
Hebrew University of Jerusalem
Shmuel Zamir
Affiliation:
Hebrew University of Jerusalem
Get access Rights & Permissions [Opens in a new window]

Abstract

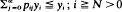For an aperiodic, irreducible Markov chain with the non-negative integers as state space it is shown that the existence of a solution to in which yi → ∞is necessary and sufficient for recurrence, and the existence of a bounded solution to the same inequalities, with yk < yo, · · ·, yN–1 for some k ≧ N, is necessary and sufficient for transience.

Keywords

RECURRENCETRANSIENCE
Type
Short Communications
Information
Journal of Applied Probability , Volume 15 , Issue 4 , December 1978 , pp. 848 - 851
Copyright
Copyright © Applied Probability Trust 1978 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chow, Y. S., Robbins, H. and Siegmund, D. (1971) Great Expectations: The Theory of Optimal Stopping. Houghton Mifflin, Boston.Google Scholar
Feller, W. (1968) An Introduction to Probability Theory and its Applications. Vol. I, 3rd edn. Wiley, New York.Google Scholar
Foster, F. G. (1953) On the stochastic matrices associated with certain queuing processes. Ann. Math. Statist. 24, 355–360.CrossRefGoogle Scholar
Harris, C. M. and Marlin, P. G. (1972) A note on feedback queues with bulk service. J. Assoc. Comput. Mach. 19, 727–733.Google Scholar
Pakes, A. G. (1969) Some conditions for ergodicity and recurrence of Markov chains. Opns Res. 17, 1058–1061.Google Scholar