Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T14:44:39.381Z Has data issue: false hasContentIssue false
  • English
  • Français

Long range dependence of heavy-tailed random functions

Part of: Stochastic processes Limit theorems

Published online by Cambridge University Press:  16 September 2021

Rafal Kulik  and
Evgeny Spodarev
Rafal Kulik*
Affiliation:
University of Ottawa
Evgeny Spodarev*
Affiliation:
Ulm University
*
*Postal address: Department of Mathematics and Statistics, 150 Louis Pasteur Private, K1N 6N5 Ottawa, Ontario, Canada.
**Postal address: Institute of Stochastics, Helmholtzstrasse 18, D-89069 Ulm, Germany. Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce a definition of long range dependence of random processes and fields on an (unbounded) index space 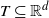$T\subseteq \mathbb{R}^d$ in terms of integrability of the covariance of indicators that a random function exceeds any given level. This definition is specifically designed to cover the case of random functions with infinite variance. We show the value of this new definition and its connection to limit theorems via some examples including subordinated Gaussian as well as random volatility fields and time series.

Keywords

Long memoryrandom processrandom fieldtime serieslevel setheavy tailinfinite varianceshort range dependencemixingsubordinated Gaussian processstochastic volatility processlimit theorem

MSC classification

Primary: 60G10: Stationary processes
Secondary: 60G60: Random fields 60G15: Gaussian processes 60F05: Central limit and other weak theorems
Type
Original Article
Information
Journal of Applied Probability , Volume 58 , Issue 3 , September 2021 , pp. 569 - 593
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. and Stegun, I. A. (eds) (1992). Handbook of Mathematical Functions, With Formulas, Graphs, and Mathematical Tables. Dover Publications, New York. Reprint of the 1972 edition.Google Scholar
Alodat, T. and Olenko, A. (2019). Asymptotic behaviour of discretized functionals of long-range dependent functional data. Available at arXiv:1905.10030v1.Google Scholar
Andersen, T., Davis, R., Kreiß, J.-P. and Mikosch, T. (eds) (2009). Handbook of Financial Time Series. Springer, Berlin.Google Scholar
Andrews, G. E., Askey, R. and Roy, R. (1999). Special Functions (Encyclopaedia Math. Appl. 71). Cambridge University Press.Google Scholar
Beran, J., Feng, Y., Ghosh, S. and Kulik, R. (2013). Long Memory Processes: Probabilistic Properties and Statistical Methods. Springer.Google Scholar
Bradley, R. C. (1983). On the $\psi $ -mixing condition for stationary random sequences. Trans. Amer. Math. Soc. 276, 55–66.Google Scholar
Bulinski, A. and Shashkin, A. (2007). Limit Theorems for Associated Random Fields and Related Systems. (Adv. Series Statist. Sci. Appl. Prob. 10). World Scientific, Hackensack, NJ.CrossRefGoogle Scholar
Bulinski, A., Spodarev, E. and Timmermann, F. (2012). Central limit theorems for the excursion sets volumes of weakly dependent random fields. Bernoulli 18, 100–118.CrossRefGoogle Scholar
CramÉr, H. (1946). Mathematical Methods of Statistics (Princeton Math. Series 9). Princeton University Press.Google Scholar
Damarackas, J. and Paulauskas, V. (2017). Spectral covariance and limit theorems for random fields with infinite variance. J. Multivariate Anal. 153, 156–175.CrossRefGoogle Scholar
Davydov, Y. and Paulauskas, V. (2018). Lamperti type theorems for random fields. Teor. Veroyatn. Primen. 63, 520–544. Reprinted in Theory Prob. Appl. 6 (2019), 426–446.CrossRefGoogle Scholar
Dehling, H. and Philipp, W. (2002). Empirical process techniques for dependent data. In Empirical Process Techniques for Dependent Data, pp. 3–113. BirkhÄuser, Boston.CrossRefGoogle Scholar
Doukhan, P. (1994). Mixing: Properties and Examples (Lecture Notes Statist. 85). Springer, New York.Google Scholar
Durante, F. and Sempi, C. (2016). Principles of Copula Theory. CRC Press, Boca Raton.Google Scholar
Giraitis, L., Koul, H. L. and Surgailis, D. (2012). Large Sample Inference for Long Memory Processes. Imperial College Press, London.CrossRefGoogle Scholar
Heinrich, L. (1996). Mixing properties and central limit theorem for a class of non-identical piecewise monotonic $C^2$ -transformations. Math. Nachr. 181, 185–214.CrossRefGoogle Scholar
Ibragimov, I. A. and Linnik, Y. V. (1971). Independent and Stationary Sequences of Random Variables. Wolters-Noordhoff, Groningen.Google Scholar
Ivanov, A. V. and Leonenko, N. N. (1989). Statistical Analysis of Random Fields. Kluwer, Dordrecht.CrossRefGoogle Scholar
Landkof, N. S. (1972). Foundations of Modern Potential Theory (Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen 180). Springer, Berlin.Google Scholar
Lavancier, F. (2006). Long memory random fields. In Dependence in Probability and Statistics (Lecture Notes Statist. 187), pp. 195–220. Springer, New York.CrossRefGoogle Scholar
Lehmann, E. L. (1966). Some concepts of dependence. Ann. Math. Statist. 37, 1137–1153.CrossRefGoogle Scholar
Leonenko, N. (1999). Limit Theorems for Random Fields with Singular Spectrum (Math. Appl. 465). Kluwer Academic Publishers, Dordrecht.Google Scholar
Leonenko, N. and Olenko, A. (2014). Sojourn measures of Student and Fisher–Snedecor random fields. Bernoulli 20, 1454–1483.CrossRefGoogle Scholar
Leonenko, N. N., Ruiz-Medina, M. D. and Taqqu, M. S. (2017). Rosenblatt distribution subordinated to Gaussian random fields with long-range dependence. Stoch. Anal. Appl. 35, 144–177.CrossRefGoogle Scholar
Makogin, V., Oesting, M., Rapp, A. and Spodarev, E. (2021). Long range dependence for stable random processes. J. Time Series Anal. 42, 161–185.CrossRefGoogle Scholar
Meschenmoser, D. and Shashkin, A. (2011). Functional central limit theorem for the volume of excursion sets generated by associated random fields. Statist. Prob. Lett. 81, 642–646.CrossRefGoogle Scholar
Owada, T. and Samorodnitsky, G. (2015). Maxima of long memory stationary symmetric $\alpha$ -stable processes, and self-similar processes with stationary max-increments. Bernoulli 21, 1575–1599.Google Scholar
Paulauskas, V. (2016). Some remarks on definitions of memory for stationary random processes and fields. Lith. Math. J. 56, 229–250.CrossRefGoogle Scholar
Rapaport, A. (2017). A dimension gap for continued fractions with independent digits: the non-stationary case. Available at arXiv:1703.03164v1.Google Scholar
Resnick, S. I. (2007). Heavy-Tail Phenomena: Probabilistic and Statistical Modeling (Springer Series in Operations Research and Financial Engineering). Springer, New York.Google Scholar
Roy, P. (2010). Nonsingular group actions and stationary $S\alpha S$ random fields. Proc. Amer. Math. Soc. 138, 2195–2202.CrossRefGoogle Scholar
Roy, P. and Samorodnitsky, G. (2008). Stationary symmetric $\alpha$ -stable discrete parameter random fields. J. Theoret. Prob. 21, 212–233.CrossRefGoogle Scholar
Rozanov, Y. A. (1967). Stationary Random Processes. Holden-Day, San Francisco, London and Amsterdam.Google Scholar
Samorodnitsky, G. (2004). Extreme value theory, ergodic theory and the boundary between short memory and long memory for stationary stable processes. Ann. Prob. 32, 1438–1468.CrossRefGoogle Scholar
Samorodnitsky, G. (2016). Stochastic Processes and Long Range Dependence (Springer Series in Operations Research and Financial Engineering). Springer, Cham.Google Scholar
Samorodnitsky, G. and Taqqu, M. S. (1994). Stable Non-Gaussian Random Processes: Stochastic Models with Infinite Variance (Stochastic Modeling). Chapman & Hall, New York.Google Scholar
Samorodnitsky, G. and Wang, Y. (2019). Extremal theory for long range dependent infinitely divisible processes. Ann. Prob. 47, 2529–2562.CrossRefGoogle Scholar
Samur, J. D. (1989). On some limit theorems for continued fractions. Trans. Amer. Math. Soc. 316, 53–79.CrossRefGoogle Scholar
Shephard, N. (ed.) (2005). Stochastic Volatility: Selected Readings. Oxford University Press.Google Scholar
Sly, A. and Heyde, C. (2008). Nonstandard limit theorem for infinite variance functionals. Ann. Prob. 36, 796–805.CrossRefGoogle Scholar
Spodarev, E. (2014). Limit theorems for excursion sets of stationary random fields. In Modern Stochastics and Applications (Springer Optim. Appl. 90), pp. 221–241. Springer, Cham.CrossRefGoogle Scholar
Steutel, F. W. and van Harn, K. (2004). Infinite Divisibility of Probability Distributions on the Real Line (Monographs Textbooks Pure Appl. Math. 259). Marcel Dekker, New York.Google Scholar
Veillette, M. S. and Taqqu, M. S. (2013). Properties and numerical evaluation of the Rosenblatt distribution. Bernoulli 19, 982–1005.CrossRefGoogle Scholar
Yaglom, A. M. (1987). Correlation Theory of Stationary and Related Random Functions, Vol. I, Basic Results (Springer Series in Statistics). Springer, New York.Google Scholar