Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Grandell, Jan
1976.
Doubly Stochastic Poisson Processes.
Vol. 529,
Issue. ,
p.
190.
Serfozo, Richard F.
1977.
Compositions, inverses and thinnings of random measures.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 37,
Issue. 3,
p.
253.
Neveu, J.
1977.
Ecole d’Eté de Probabilités de Saint-Flour VI-1976.
Vol. 598,
Issue. ,
p.
249.
BRILLINGER, DAVID R.
1978.
Vol. 1,
Issue. ,
p.
33.
Karr, A.F.
1978.
Derived random measures.
Stochastic Processes and their Applications,
Vol. 8,
Issue. 2,
p.
159.
Brown, Tim
1979.
Position dependent and stochastic thinning of point processes.
Stochastic Processes and their Applications,
Vol. 9,
Issue. 2,
p.
189.
Waymire, Ed
and
Gupta, Vijay K.
1981.
The mathematical structure of rainfall representations: 2. A review of the theory of point processes.
Water Resources Research,
Vol. 17,
Issue. 5,
p.
1273.
Böker, Fred
and
Serfozo, Richard
1983.
Ordered thinnings of point processes and random measures.
Stochastic Processes and their Applications,
Vol. 15,
Issue. 2,
p.
113.
Galbraith, R. F.
1984.
On statistical estimation in fission track dating.
Journal of the International Association for Mathematical Geology,
Vol. 16,
Issue. 7,
p.
653.
Thall, Peter F.
1984.
A theorem on regular infinitely divisible cox processes.
Stochastic Processes and their Applications,
Vol. 16,
Issue. 2,
p.
205.
Serfozo, Richard F.
1984.
Rarefactions of compound point processes.
Journal of Applied Probability,
Vol. 21,
Issue. 4,
p.
710.
Böker, Fred
1984.
A thinning result for pure jump processes.
Stochastic Processes and their Applications,
Vol. 16,
Issue. 2,
p.
171.
Chandramohan, Jagadeesh
Foley, Robert D.
and
Disney, Ralph L.
1985.
Thinning of point processes—covariance analyses.
Advances in Applied Probability,
Vol. 17,
Issue. 1,
p.
127.
Karr, Alan F
1985.
Inference for thinned point processes, with application to Cox processes.
Journal of Multivariate Analysis,
Vol. 16,
Issue. 3,
p.
368.
Böker, Fred
1985.
Limits of generalized compound point processes.
Statistics,
Vol. 16,
Issue. 1,
p.
97.
Todorovic, P.
and
Woolhiser, D. A.
1987.
Flood Hydrology.
p.
143.
Yannaros, Nikos
1989.
On Cox and renewal processes.
Statistics & Probability Letters,
Vol. 7,
Issue. 5,
p.
431.
Rogosa, David
and
Ghandour, Ghassan
1991.
Statistical Models for Behavioral Observations.
Journal of Educational Statistics,
Vol. 16,
Issue. 3,
p.
157.
Embrechts, P.
and
Klüppelberg, C.
1994.
Some Aspects of Insurance Mathematics.
Theory of Probability & Its Applications,
Vol. 38,
Issue. 2,
p.
262.
Aissani, A.
1997.
Limit distributions for dependent thinning of dissipative point processes.
Microelectronics Reliability,
Vol. 37,
Issue. 2,
p.
267.
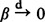 . In the particular case when β takes the values 1 and 0 with probabilities p and 1 –p respectively, ξ becomes a p-thinning of η and our theorems contain some classical results by Rényi and others on the thinnings of a fixed process, as well as a characterization by Mecke of the class of subordinated Poisson processes.
. In the particular case when β takes the values 1 and 0 with probabilities p and 1 –p respectively, ξ becomes a p-thinning of η and our theorems contain some classical results by Rényi and others on the thinnings of a fixed process, as well as a characterization by Mecke of the class of subordinated Poisson processes.