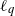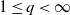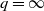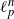Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kabluchko, Zakhar
Prochno, Joscha
and
Sonnleitner, Mathias
2025.
A probabilistic approach to Lorentz balls ℓq,1n.
Journal of Functional Analysis,
Vol. 288,
Issue. 1,
p.
110682.