Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-22T00:41:45.639Z Has data issue: false hasContentIssue false
  • English
  • Français

Limit distributions of the number of renewals and waiting times

Published online by Cambridge University Press:  14 July 2016

N. R. Mohan
N. R. Mohan*
Affiliation:
University of Mysore
Get access Rights & Permissions [Opens in a new window]

Abstract

Let {Xn} be an infinite sequence of independent non-negative random variables. Let the distribution function of Xi, i = 1, 2, …, be either F1 or F2 where F1 and F2 are distinct. Set Sn = X1 + X2 + … + Xn and for t > 0 define 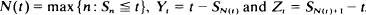and Zt = SN(t)+1 – t. The limit distributions of N(t), Yt and Zt as t → ∞ are obtained when F1 and F2 are in the domains of attraction of stable laws with exponents α1 and α2, respectively and Sn properly normalised has the composition of these two stable laws as its limit distribution.

Keywords

RENEWALSPENT AND RESIDUAL WAITING TIMESREGULARLY AND SLOWLY VARYING FUNCTIONSCOMPOSITION OF STABLE LAWSDOMAIN OF ATTRACTIONSAMPLING SCHEMEKARAMATA'S REPRESENTATIONTAUBERIAN THEOREM
Type
Research Papers
Information
Journal of Applied Probability , Volume 13 , Issue 2 , June 1976 , pp. 301 - 312
Copyright
Copyright © Applied Probability Trust 1976 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Gnedenko, B. V. and Kolmogorov, A. N. (1954) Limit Distributions for Sums of Independent Random Variables. Addison-Wesley, Cambridge, Mass.Google Scholar
[2] Feller, W. (1966) An Introduction to Probability Theory and its Applications , Vol. II. Wiley, New York.Google Scholar
[3] Pakshirajan, R. P. and Vasudeva, R. On the limit distribution of sums of independent random variables. Unpublished.Google Scholar
[4] Prabhu, N. U. (1965) Stochastic Processes. MacMillan, New York.Google Scholar
[5] Smith, W. L. (1968) On infinitely divisible laws and a renewal theorem for non-negative random variables. Ann. Math. Statist. 39, 139–154.CrossRefGoogle Scholar
[6] Sreehari, M. (1970) On a class of limit distributions for normalized sums of independent random variables. Theor. Prob. Appl. 15, 258–281.CrossRefGoogle Scholar