Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Glynn, Peter W.
and
Zeevi, Assaf J.
2000.
On the maximum workload of a queue fed by fractional Brownian motion.
The Annals of Applied Probability,
Vol. 10,
Issue. 4,
Norros, Ilkka
2002.
NETWORKING 2002: Networking Technologies, Services, and Protocols; Performance of Computer and Communication Networks; Mobile and Wireless Communications.
Vol. 2345,
Issue. ,
p.
86.
Lee, Jiyeon
2002.
Fluid Queueing Model with Fractional Brownian Input.
Communications for Statistical Applications and Methods,
Vol. 9,
Issue. 3,
p.
649.
Mannersalo, Petteri
and
Norros, Ilkka
2002.
A most probable path approach to queueing systems with general Gaussian input.
Computer Networks,
Vol. 40,
Issue. 3,
p.
399.
Erramilli, A.
Roughan, M.
Veitch, D.
and
Willinger, W.
2002.
Self-similar traffic and network dynamics.
Proceedings of the IEEE,
Vol. 90,
Issue. 5,
p.
800.
Addie, Ron
Mannersalo, Petteri
and
Norros, Ilkka
2002.
Most probable paths and performance formulae for buffers with gaussian input traffic.
European Transactions on Telecommunications,
Vol. 13,
Issue. 3,
p.
183.
Harmantzis, F.C.
Hatzinakos, D.
and
Lambadaris, I.
2003.
Effective bandwidths and tail probabilities for Gaussian and stable self-similar traffic.
Vol. 3,
Issue. ,
p.
1515.
Guoqiang Mao
2003.
Finite timescale range of interest for self-similar traffic measurements, modelling and performance analysis.
p.
7.
Duffy, Ken
Lewis, John T.
and
Sullivan, Wayne G.
2003.
Logarithmic asymptotics for the supremum of a stochastic process.
The Annals of Applied Probability,
Vol. 13,
Issue. 2,
Lelarge, M.
Liu, Z.
and
Xia, C.H.
2004.
Asymptotic tail distribution of end-to-end delay in networks of queues with self-similar cross traffic.
Vol. 4,
Issue. ,
p.
2352.
Ben Azzouna, Nadia
Clérot, Fabrice
Fricker, Christine
and
Guillemin, Fabrice
2004.
A flow-based approach to modeling ADSL traffic on an IP backbone link.
Annales des Télécommunications,
Vol. 59,
Issue. 11-12,
p.
1260.
Mandjes, Michel
and
Boots, Nam Kyoo
2004.
The Shape of the Loss Curve and the Impact of Long-Range Dependence on Network Performance.
AEU - International Journal of Electronics and Communications,
Vol. 58,
Issue. 2,
p.
101.
Janowski, L.
and
Papir, Z.
2005.
Analysis of a burstiness curve for FBM traffic and token bucket shaping algorithm.
p.
439.
Dieker, A.B.
2005.
Extremes of Gaussian processes over an infinite horizon.
Stochastic Processes and their Applications,
Vol. 115,
Issue. 2,
p.
207.
Rolls, D.A.
Michailidis, G.
and
Hernández-Campos, F.
2005.
Queueing analysis of network traffic: methodology and visualization tools.
Computer Networks,
Vol. 48,
Issue. 3,
p.
447.
Wicker, Fletcher
2006.
QoS for Space Based Routers Serving Downlinks with Time Varying Data Rates.
Ribeiro, V.J.
Riedi, R.H.
and
Baraniuk, R.G.
2006.
Multiscale Queueing Analysis.
IEEE/ACM Transactions on Networking,
Vol. 14,
Issue. 5,
p.
1005.
Li, Hailong
and
Thng, Ian Li-Jin
2006.
Edge node buffer usage in optical burst switching networks.
Photonic Network Communications,
Vol. 13,
Issue. 1,
p.
31.
Cheng, Yu
Zhuang, Weihua
and
Wang, Lei
2007.
Calculation of Loss Probability in a Finite Size Partitioned Buffer for Quantitative Assured Service.
IEEE Transactions on Communications,
Vol. 55,
Issue. 9,
p.
1757.
Li, Hailong
and
Thng, Ian Li-Jin
2007.
Edge node buffer usage in optical burst switching networks.
Photonic Network Communications,
Vol. 13,
Issue. 1,
p.
31.
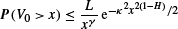 for large x. Explicit formulae for constants κ, γ and L are given in terms of H and system parameters.
for large x. Explicit formulae for constants κ, γ and L are given in terms of H and system parameters.