Article contents
Inequalities for the M/G/∞ queue and related shot noise processes
Published online by Cambridge University Press: 14 July 2016
Abstract
Suppose that pulses arrive according to a Poisson process of rate λ with the duration of each pulse independently chosen from a distribution F having finite mean. Let X(t) be the shot noise process formed by the superposition of these pulses. We consider functionals H(X) of the sample path of X(t). H is said to be L-superadditive if 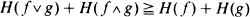 for all functions f and g. For any distribution F for the pulse durations, we define H(F) = EH(X). We prove that if H is L-superadditive and
for all functions f and g. For any distribution F for the pulse durations, we define H(F) = EH(X). We prove that if H is L-superadditive and 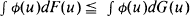 for all convex functions ϕ, then
for all convex functions ϕ, then 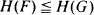 . Various consequences of this result are explored.
. Various consequences of this result are explored.
- Type
- Research Papers
- Information
- Copyright
- Copyright © Applied Probability Trust 1987
Footnotes
Research supported by the Office of Naval Research under contract N00014-76-C-0475.
References
- 7
- Cited by


