Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Schiefermayr, Klaus
2003.
Random walks with similar transition probabilities.
Journal of Computational and Applied Mathematics,
Vol. 153,
Issue. 1-2,
p.
423.
van Doorn, Erik A.
2003.
Birth–death processes and associated polynomials.
Journal of Computational and Applied Mathematics,
Vol. 153,
Issue. 1-2,
p.
497.
2004.
Birth and Death (BDP) Process Models with Applications.
American Journal of Mathematical and Management Sciences,
Vol. 24,
Issue. 1-2,
p.
1.
van Doorn, Erik A.
and
Zeifman, Alexander I.
2005.
Birth-death processes with killing.
Statistics & Probability Letters,
Vol. 72,
Issue. 1,
p.
33.
Parthasarathy, P. R.
and
Sudhesh, R.
2006.
Exact transient solution of a state‐dependent birth‐death process.
International Journal of Stochastic Analysis,
Vol. 2006,
Issue. 1,
Crescenzo, Antonio Di
and
Martinucci, Barbara
2008.
A First-Passage-Time Problem for Symmetric and Similar Two-Dimensional Birth–Death Processes.
Stochastic Models,
Vol. 24,
Issue. 3,
p.
451.
Di Crescenzo, Antonio
and
Martinucci, Barbara
2009.
On a Symmetric, Nonlinear Birth-Death Process with Bimodal Transition Probabilities.
Symmetry,
Vol. 1,
Issue. 2,
p.
201.
Heidergott, Bernd
Hordijk, Arie
and
Leder, Nicole
2010.
Series Expansions for Continuous-Time Markov Processes.
Operations Research,
Vol. 58,
Issue. 3,
p.
756.
Poskrobko, Anna
and
Girejko, Ewa
2015.
Families of ν-similar birth-death processes and limiting conditional distributions.
Advances in Difference Equations,
Vol. 2015,
Issue. 1,
Di Crescenzo, Antonio
Giorno, Virginia
and
Nobile, Amelia G.
2016.
Constructing transient birth–death processes by means of suitable transformations.
Applied Mathematics and Computation,
Vol. 281,
Issue. ,
p.
152.
Giorno, Virginia
and
Nobile, Amelia G.
2019.
First-passage times and related moments for continuous-time birth–death chains.
Ricerche di Matematica,
Vol. 68,
Issue. 2,
p.
629.
Giorno, Virginia
and
Nobile, Amelia G.
2020.
On a class of birth-death processes with time-varying intensity functions.
Applied Mathematics and Computation,
Vol. 379,
Issue. ,
p.
125255.
Giorno, Virginia
and
Nobile, Amelia G.
2020.
Bell Polynomial Approach for Time-Inhomogeneous Linear Birth–Death Process with Immigration.
Mathematics,
Vol. 8,
Issue. 7,
p.
1123.
Giorno, Virginia
and
Nobile, Amelia G.
2022.
On some integral equations for the evaluation of first-passage-time densities of time-inhomogeneous birth-death processes.
Applied Mathematics and Computation,
Vol. 422,
Issue. ,
p.
126993.
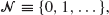 but allow the death rate in state 0 to be positive, so that escape from
but allow the death rate in state 0 to be positive, so that escape from 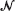 is possible. Two such processes with transition functions
is possible. Two such processes with transition functions 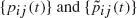 are said to be similar if, for all
are said to be similar if, for all 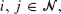 there are constants cij such that
there are constants cij such that 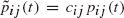 for all t ≥ 0. We determine conditions on the birth and death rates of a birth-death process for the process to be a member of a family of similar processes, and we identify the members of such a family. These issues are also resolved in the more general setting in which the two processes are called similar if there are constants cij and ν such that
for all t ≥ 0. We determine conditions on the birth and death rates of a birth-death process for the process to be a member of a family of similar processes, and we identify the members of such a family. These issues are also resolved in the more general setting in which the two processes are called similar if there are constants cij and ν such that 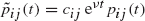 for all t ≥ 0.
for all t ≥ 0.