Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T14:46:30.716Z Has data issue: false hasContentIssue false
  • English
  • Français

Extinction time of the logistic process

Part of: Stochastic processes Special processes

Published online by Cambridge University Press:  16 September 2021

Eric Foxall
Eric Foxall*
Affiliation:
University of British Columbia, Okanagan Campus
*
*Postal address: 3333 University Way, Kelowna BC Canada V1V 1V7. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

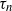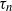The logistic birth and death process is perhaps the simplest stochastic population model that has both density-dependent reproduction and a phase transition, and a lot can be learned about the process by studying its extinction time, $\tau_n$ , as a function of system size n. A number of existing results describe the scaling of $\tau_n$ as 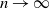$n\to\infty$ for various choices of reproductive rate 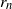$r_n$ and initial population 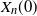$X_n(0)$ as a function of n. We collect and complete this picture, obtaining a complete classification of all sequences 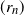$(r_n)$ and 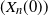$(X_n(0))$ for which there exist rescaling parameters 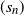$(s_n)$ and 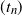$(t_n)$ such that 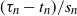$(\tau_n-t_n)/s_n$ converges in distribution as 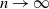$n\to\infty$ , and identifying the limits in each case.

Keywords

SIS modelstochastic logistic modeldiffusion approximationlarge deviationsphase transition

MSC classification

Primary: 60G99: None of the above, but in this section
Secondary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Type
Original Article
Information
Journal of Applied Probability , Volume 58 , Issue 3 , September 2021 , pp. 637 - 676
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersson, H. and Djehiche, B. (1998). A threshold limit theorem for the stochastic logistic epidemic. J. Appl. Prob. 35, 662–670.10.1239/jap/1032265214CrossRefGoogle Scholar
Athreya, K. B. and Ney, P. E. (1972). Branching Processes. Springer, Berlin.10.1007/978-3-642-65371-1CrossRefGoogle Scholar
Barbour, A. D., Chigansky, P. and Klebaner, F. (2015). On the emergence of random initial conditions in fluid limits. J. Appl. Prob. 53, 1193–1205.10.1017/jpr.2016.74CrossRefGoogle Scholar
Basak, A., Durrett, R. and Foxall, E. (2018). Diffusion limit for the partner model at the critical value. Electron. J. Prob. 23, 102.CrossRefGoogle Scholar
Brightwell, G., House, T., and Luczak, M. (2018). Extinction times in the subcritical stochastic SIS logistic epidemic. J. Math. Biol. 77, 455–493.10.1007/s00285-018-1210-5CrossRefGoogle ScholarPubMed
Doering, C. R., Sargsyan, K. V. and Sander, L. M. (2005). Extinction times for birth–death processes: Exact results, continuum asymptotics, and the failure of the Fokker–Planck approximation. Multiscale Model Simul. 3, 283–299.CrossRefGoogle Scholar
Dolgoarshinnykh, R. G. and Lalley, S. P. (2006). Critical scaling for the SIS stochastic epidemic. J. Appl. Prob. 43, 892–898.CrossRefGoogle Scholar
Durrett, R. (2010). Probability: Theory and Examples, 4th edn. Cambridge University Press.CrossRefGoogle Scholar
Ethier, S. N., and Kurtz, T. G. (1986). Markov Processes: Characterization and Convergence. John Wiley, New York.10.1002/9780470316658CrossRefGoogle Scholar
Feller, W. (1939). Die Grundlagen der Volterraschen Theorie des Kampfes ums Dasein in wahrscheinlichkeitstheoretischer Behandlung. Acta Biotheoretica 5, 11–40.10.1007/BF01602932CrossRefGoogle Scholar
Feller, W. (2015). Selected Papers, Vol. I. Springer, New York.Google Scholar
Foxall, E. (2018). The naming game on the complete graph. Electron. J. Prob. 23, 126.10.1214/18-EJP250CrossRefGoogle Scholar
Jacod, J. and Shiryaev, A. N. (2002). Limit Theorems for Stochastic Processes. Springer, New York.Google Scholar
Kallenberg, O. (1997). Foundations of Modern Probability. Springer, New York.Google Scholar
Keilson, J. (1979). Markov Chain Models: Rarity and Exponentiality (Appl. Math. Sci. 28). Springer, New York.10.1007/978-1-4612-6200-8CrossRefGoogle Scholar
Kryscio, R. J. and LefÉvre, C. (1989). On the extinction of the S-I-S stochastic logistic epidemic. J. Appl. Prob. 26, 685–694.CrossRefGoogle Scholar
Kurtz, T. G. (1978). Strong approximation theorems for density-dependent Markov chains. Stoch. Process. Appl. 6, 223–240.10.1016/0304-4149(78)90020-0CrossRefGoogle Scholar
Nasell, I. (1996). The quasi-stationary distribution of the closed endemic SIS model. Adv. Appl. Prob. 28, 895–932.CrossRefGoogle Scholar
Nasell, I. (1999). On the quasi-stationary distribution of the stochastic logistic epidemic. Math. Biosci. 156, 21–40.CrossRefGoogle ScholarPubMed
Nasell, I. (2011). Extinction and Quasi-Stationarity in the Stochastic Logistic SIS Model. Springer, New York.10.1007/978-3-642-20530-9CrossRefGoogle Scholar
Talvila, E. and Wiersma, M. (2012). Simple derivation of basic quadrature formulas. arXiv:1202.0249.Google Scholar