Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kyriakidis, E.G.
and
Abakuks, Andris
1989.
Optimal pest control through catastrophes.
Journal of Applied Probability,
Vol. 26,
Issue. 04,
p.
873.
Bartoszynski, R.
Bühler, W. J.
Chan, Wenyaw
and
Pearl, D. K.
1989.
Population processes under the influence of disasters occurring independently of population size.
Journal of Mathematical Biology,
Vol. 27,
Issue. 2,
p.
167.
Kennedy, D. P.
1994.
On the Regularity of Skip-Free Markov Chains.
Probability in the Engineering and Informational Sciences,
Vol. 8,
Issue. 3,
p.
377.
Chao, Xiuli
1995.
A queueing network model with catastrophes and product form solution.
Operations Research Letters,
Vol. 18,
Issue. 2,
p.
75.
Al-Eideh, Basel M.
1996.
The extinction time of a diffusion model with beta-distributed catastrophe sizes.
Journal of Information and Optimization Sciences,
Vol. 17,
Issue. 2,
p.
227.
Gómez-Corral, A.
2002.
On a tandem G-network with blocking.
Advances in Applied Probability,
Vol. 34,
Issue. 3,
p.
626.
Economou, Antonis
and
Fakinos, Demetrios
2003.
A continuous-time Markov chain under the influence of a regulating point process and applications in stochastic models with catastrophes.
European Journal of Operational Research,
Vol. 149,
Issue. 3,
p.
625.
Economou, Antonis
2003.
On the control of a compound immigration process through total catastrophes.
European Journal of Operational Research,
Vol. 147,
Issue. 3,
p.
522.
Reluga, Timothy C.
2004.
Analysis of periodic growth–disturbance models.
Theoretical Population Biology,
Vol. 66,
Issue. 2,
p.
151.
Kyriakidis, E.G.
2004.
Optimal control of a simple immigration–emigration process through total catastrophes.
European Journal of Operational Research,
Vol. 155,
Issue. 1,
p.
198.
Economou, Antonis
2004.
The compound Poisson immigration process subject to binomial catastrophes.
Journal of Applied Probability,
Vol. 41,
Issue. 02,
p.
508.
Chen, Anyue
Pollett, Phil
Zhang, Hanjun
and
Cairns, Ben
2005.
Uniqueness criteria for continuous-time Markov chains with general transition structures.
Advances in Applied Probability,
Vol. 37,
Issue. 4,
p.
1056.
Cairns, B.J.
and
Pollett, P.K.
2005.
Approximating persistence in a general class of population processes.
Theoretical Population Biology,
Vol. 68,
Issue. 2,
p.
77.
Wu, Bo
and
Zhang, Yu-Hui
2007.
A Class of Multidimensional Q-Processes.
Journal of Applied Probability,
Vol. 44,
Issue. 01,
p.
226.
Al-Eideh, Basel M.
2007.
Population Moments of a Birth and Death Diffusion Model with Immigration and General Catastrophe Process.
p.
539.
Di Crescenzo, A.
Giorno, V.
Nobile, A.G.
and
Ricciardi, L.M.
2008.
A note on birth–death processes with catastrophes.
Statistics & Probability Letters,
Vol. 78,
Issue. 14,
p.
2248.
Economou, Antonis
and
Fakinos, Demetris
2008.
Alternative Approaches for the Transient Analysis of Markov Chains with Catastrophes.
Journal of Statistical Theory and Practice,
Vol. 2,
Issue. 2,
p.
183.
Baumann, Hendrik
and
Sandmann, Werner
2012.
Steady state analysis of level dependent quasi-birth-and-death processes with catastrophes.
Computers & Operations Research,
Vol. 39,
Issue. 2,
p.
413.
Keller, Peter
and
Valleriani, Angelo
2012.
Single-molecule stochastic times in a reversible bimolecular reaction.
The Journal of Chemical Physics,
Vol. 137,
Issue. 8,
Leite, Maria Conceição A.
Petrov, Nikola P.
and
Weng, Ensheng
2012.
Stationary distributions of semistochastic processes with disturbances at random times and with random severity.
Nonlinear Analysis: Real World Applications,
Vol. 13,
Issue. 2,
p.
497.
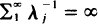 . Necessary and sufficient conditions for certain extinction of the population are derived. The results are applied to the linear birth and death process (λ j = jλ, µj = jμ) with catastrophes of several different types.
. Necessary and sufficient conditions for certain extinction of the population are derived. The results are applied to the linear birth and death process (λ j = jλ, µj = jμ) with catastrophes of several different types.