Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-04T19:46:29.178Z Has data issue: false hasContentIssue false
  • English
  • Français

Exponential convergence to a quasi-stationary distribution for birth–death processes with an entrance boundary at infinity

Part of: Markov processes Probability theory on algebraic and topological structures Ergodic theory

Published online by Cambridge University Press:  10 August 2022

Guoman He  and
Hanjun Zhang
Guoman He*
Affiliation:
Hunan University of Technology and Business
Hanjun Zhang*
Affiliation:
Xiangtan University
*
*Postal address: School of Science & Key Laboratory of Hunan Province for Statistical Learning and Intelligent Computation, Hunan University of Technology and Business, Changsha, Hunan 410205, PR China. Email address: [email protected]
**Postal address: School of Mathematics and Computational Science, Xiangtan University, Xiangtan, Hunan 411105, PR China. Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the quasi-stationary behavior of the birth–death process with an entrance boundary at infinity. We give by the h-transform an alternative and simpler proof for the exponential convergence of conditioned distributions to a unique quasi-stationary distribution in the total variation norm. In addition, we also show that starting from any initial distribution the conditional probability converges to the unique quasi-stationary distribution exponentially fast in the 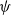$\psi$ -norm.

Keywords

Birth–death processesquasi-stationary distributionh-transformrate of convergence

MSC classification

Primary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.)
Secondary: 60B10: Convergence of probability measures 37A25: Ergodicity, mixing, rates of mixing
Type
Original Article
Information
Journal of Applied Probability , Volume 59 , Issue 4 , December 2022 , pp. 983 - 991
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, W. J. (1991). Continuous-Time Markov Chains: An Applications-Oriented Approach. Springer, New York.CrossRefGoogle Scholar
Champagnat, N. and Villemonais, D. (2016). Exponential convergence to quasi-stationary distribution and Q-process. Prob. Theory Relat. Fields 164, 243–283.CrossRefGoogle Scholar
Champagnat, N. and Villemonais, D. (2018). Uniform convergence of conditional distributions for absorbed one-dimensional diffusions. Adv. Appl. Prob. 50, 178–203.CrossRefGoogle Scholar
Chen, M.-F. (2000). Equivalence of exponential ergodicity and $\mathbb{L}^2$ -exponential convergence for Markov chains. Stochastic Process. Appl. 87, 281–297.CrossRefGoogle Scholar
Chen, M.-F. (2010). Speed of stability for birth–death processes. Front. Math. China 5, 379–515.CrossRefGoogle Scholar
Collet, P., Martnez, S. and San Martn, J. (2013). Quasi-Stationary Distributions: Markov Chains, Diffusions and Dynamical Systems. Springer, Heidelberg.CrossRefGoogle Scholar
Diaconis, P. and Miclo, L. (2015). On quantitative convergence to quasi-stationarity. Ann. Fac. Sci. Toulouse Math. 24, 973–1016.CrossRefGoogle Scholar
Gao, W.-J. and Mao, Y.-H. (2015). Quasi-stationary distribution for the birth–death process with exit boundary. J. Math. Anal. Appl. 427, 114–125.CrossRefGoogle Scholar
He, G., Zhang, H. and Zhu, Y. (2019). On the quasi-ergodic distribution of absorbing Markov processes. Statist. Prob. Lett. 149, 116–123.CrossRefGoogle Scholar
Karlin, S. and McGregor, J. L. (1957). The classification of birth and death processes. Trans. Amer. Math. Soc. 86, 366–400.CrossRefGoogle Scholar
Martnez, S., San Martn, J. and Villemonais, D. (2014). Existence and uniqueness of a quasistationary distribution for Markov processes with fast return from infinity. J. Appl. Prob. 51, 756–768.CrossRefGoogle Scholar
Méléard, S. and Villemonais, D. (2012). Quasi-stationary distributions and population processes. Prob. Surv. 9, 340–410.CrossRefGoogle Scholar
Oçafrain, W. (2020). Polynomial rate of convergence to the Yaglom limit for Brownian motion with drift. Electron. Commun. Prob. 25, 1–12.CrossRefGoogle Scholar
Oçafrain, W. (2021). Convergence to quasi-stationarity through Poincaré inequalities and Bakry–Émery criteria. Electron. J. Prob. 26, 1–30.CrossRefGoogle Scholar
Takeda, M. (2019). Existence and uniqueness of quasi-stationary distributions for symmetric Markov processes with tightness property. J. Theor. Prob. 32, 2006–2019.CrossRefGoogle Scholar
van Doorn, E. A. (1991). Quasi-stationary distributions and convergence to quasi-stationarity of birth–death processes. Adv. Appl. Prob. 23, 683–700.CrossRefGoogle Scholar
Villemonais, D. (2015). Minimal quasi-stationary distribution approximation for a birth and death process. Electron. J. Prob. 20, 1–18.CrossRefGoogle Scholar
Zhang, H. and Zhu, Y. (2013). Domain of attraction of the quasistationary distribution for birth-and-death processes. J. Appl. Prob. 50, 114–126.CrossRefGoogle Scholar