Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T09:33:49.881Z Has data issue: false hasContentIssue false
  • English
  • Français

Divergent population processes and mammal outbreaks

Published online by Cambridge University Press:  14 July 2016

P. Holgate
P. Holgate*
Affiliation:
The Nature Conservancy, London
Get access Rights & Permissions [Opens in a new window]

Extract

Birth and death processes, i.e. Markov chains {X(t)}, 0 ≦ t ≦ ∞, taking values in the set I of non-negative integers, for which the infinitesimal transition probabilities are 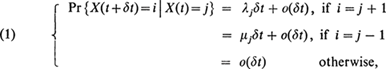have found wide application in mathematical ecology . In order that the infinite system of differential Equations (1) should have solutions 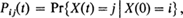such that Pij(t) ≦ 0, all t and 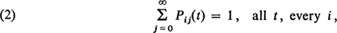it is necessary and sufficient that 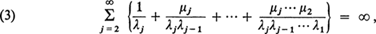. The conditions ensure that with probability one, the sample paths of X(t) have no discontinuities worse than jumps, and in this case the solution is unique. If (3) does not hold then for some t1 at least, there is a set of sample paths of positive probability, each of which has t1 as a limit point of jumps. For pure birth processes, (in which μj = 0) this clearly implies X(t) → ∞ as t → t1.

Type
Research Papers
Information
Journal of Applied Probability , Volume 4 , Issue 1 , November 1967 , pp. 1 - 8
Copyright
Copyright © Applied Probability Trust 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Bartlett, M. S. (1949) Some evolutionary stochastic processes. J. R. Statist. Soc. B 11, 211–229.Google Scholar
[2] Bartlett, M. S. (1955) Stochastic Processes. Cambridge.Google Scholar
[3] Bartlett, M. S. (1960) Stochastic Population Models. Methuen, London.Google Scholar
[4] Boyd, J. M., Doney, J., Gunn, R. G. and Jewell, P. A. (1964) The Soay sheep of the island of Hirta, St. Kilda. Proc. Zool. Soc. London 142, 129–163.Google Scholar
[5] Chung, K. L. (1960) Markov Chains with Stationary Transition Probabilities. Springer, Berlin.Google Scholar
[6] Davies, H. T., (Ed.) (1935) Tables of the Higher Transcendental Functions 2. Bloomington, Indiana.Google Scholar
[7] Doob, J. L. (1945) Markov chains-denumerable case. Trans. Amer. Math. Soc. 58, 455–473.Google Scholar
[8] Elton, C. (1942) Voles, Mice and Lemmings. Oxford (reprinted 1965, J. Cramer, Weinheim).Google Scholar
[9] Erdelyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F. G. (1953) Higher Transcendental Functions. McGraw-Hill, New York.Google Scholar
[10] Feller, W. (1940) On the integro-differential equations of purely discontinuous Markoff Processes. Trans. Amer. Math. Soc. 48, 488–575.Google Scholar
[11] Feller, W. (1954) Diffusion processes in one dimension. Trans. Amer. Math. Soc. 77, 1–31.Google Scholar
[12] Frazer-Darling, F. (1938) Bird Flocks and the Breeding Cycle. Cambridge.Google Scholar
[13] John, P. W. M. (1957) Divergent time homogenous birth and death processes. Ann. Math. Statist. 28, 514–517.Google Scholar
[14] John, P. W. M. (1961) A note on the quadratic birth process. J. London Math. Soc. 36, 159–160 Google Scholar
[15] Kendall, D. G. (1949) Stochastic processes and population growth. J. R. Statist. Soc. B 11, 230–264.Google Scholar
[16] Reuter, G. E. H. (1947) Denumerable Markov processes and the associated contraction semi-groups on 1. Acta Math. 97, 1–46.Google Scholar
[17] Reuter, G. E. H. and Lederman, W. (1953) On the differential equations of the transition probabilities of Markov processes with enumerably many states. Proc. Camb. Phil. Soc. 49, 247–262.Google Scholar