Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-29T01:21:57.989Z Has data issue: false hasContentIssue false
  • English
  • Français

Deviations from monotonicity of a Wiener process with drift

Published online by Cambridge University Press:  14 July 2016

P. J. Brockwell
P. J. Brockwell*
Affiliation:
Michigan State University
*
*Now at La Trobe University.
Get access Rights & Permissions [Opens in a new window]

Abstract

If X(t) is a Wiener process with EX(t) = vt and var X(t) = σ2t (where v > 0) and if M(t) = max0≦τ≦tX(τ) and Ta is the time of first passage through level a (where a > 0) we show that 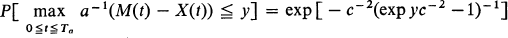where 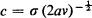is the coefficient of variation of Ta. Applications of the result to the “maturity-time” representation of cell-growth and to queues with heavy traffic are discussed.

Keywords

WIENER PROCESS WITH DRIFTRANDOM WALKWEAK CONVERGENCECELL-GROWTHQUEUES WITH HEAVY TRAFFIC
Type
Short Communications
Information
Journal of Applied Probability , Volume 11 , Issue 1 , March 1974 , pp. 206 - 210
Copyright
Copyright © Applied Probability Trust 1974 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported by Air Force Office of Scientific Research under AFOSR Contract F44620–67–C–0049 in the Department of Mathematics, Stanford University.

References

[1] Billingsley, P. (1968) Convergence of Probability Measures. John Wiley, New York.Google Scholar
[2] Brockwell, P. J. and Trucco, E. (1970) On the decomposition by generations of the PLM-function. J. Theoret. Biol. 26,149–179.CrossRefGoogle ScholarPubMed
[3] Cox, D. R. and Miller, H. D. (1965) The Theory of Stochastic Processes. Methuen, London.Google Scholar
[4] Iglehart, D. I. and Whitt, W. (1970) Multiple channel queues in heavy traffic II: sequences, networks and batches Adv. Appl. Prob. 2, 355–369.CrossRefGoogle Scholar
[5] Rubinow, S. I. (1968) Maturity-time representation for cell populations Biophys. J. 8, 1055–1073.CrossRefGoogle ScholarPubMed
[6] Stone, C. (1963) Weak convergence of stochastic processes defined on semi-infinite intervals Proc. Amer. Math. Soc. 14, 694–696.CrossRefGoogle Scholar
[7] Stuart, R. N. and Merkle, T. C. (1965) The calculation of treatment schedules for cancer chemotherapy, Part II. UCRL–14505–2, Lawrence Radiation Laboratory, Livermore, Ca. Google Scholar
[8] Whitt, W. (1971) Weak convergence of first passage time processes. J. Appl. Prob. 8 417–422.CrossRefGoogle Scholar