Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T14:08:43.838Z Has data issue: false hasContentIssue false
  • English
  • Français

Convergence rate for the distributions of GI/M/1/n and M/GI/1/n as n tends to infinity

Published online by Cambridge University Press:  14 July 2016

F. Simonot
F. Simonot*
Affiliation:
ESSTIN
*
∗Postal address: ESSTIN – Parc R. Bentz, 54500, Vandoeuvre, France. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this note, we compare the arrival and time stationary distributions of the number of customers in the GI/M/1/n and GI/M/1 queueing systems. We show that, if the inter-arrival c.d.f. H is non-lattice with mean value λ –1, and if the traffic intensity ρ = λμ –1 is strictly less than one, then the convergence rate of the stationary distributions of GI/M/1/n to the corresponding stationary distributions of GI/M/1 is geometric. More-over, the convergence rate can be characterized by the number ω, the unique solution in (0, 1) of the equation . 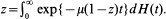A similar result is established for the M/GI/1/n and M/GI/1 queueing systems.

Keywords

GI/M/1/nM/GI/1/n; MARKOV CHAINLINDLEY PROCESSCOUPLINGCONVERGENCE RATE
Type
Research Papers
Information
Journal of Applied Probability , Volume 34 , Issue 4 , December 1997 , pp. 1049 - 1060
Copyright
Copyright © Applied Probability Trust 1997 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asmussen, S. (1981) Equilibrium properties of the M/G/1 queue. Z. Wahrscheinlichkeitsth. 58, 267–281.CrossRefGoogle Scholar
Asmussen, S. (1987) Applied Probability and Queues. Wiley, New York.Google Scholar
Billingsley, P. (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
Daley, D. J. (1968) Stochastically monotone Markov chains. Z. Wahrscheinlichkeitsth. 10, 305–307.Google Scholar
Gibson, D. and Seneta, E. (1987) Monotone infinite stochastic matrices and their augmented truncations. Stoch. Proc. Appl. 24, 287–292.CrossRefGoogle Scholar
Heyman, D. P. (1991) Approximating the stationary distribution of an infinite stochastic matrix. J. Appl. Prob. 28, 96–103.Google Scholar
Heyman, D. P. and Whitt, W. (1989) Limits of queues as the waiting room grows. Queueing Systems 5, 381–392.Google Scholar
Kalashnikov, V. V. and Rachev, S. T. (1990) Mathematical Methods for Construction of Queueing Models. Wadsworth and Brooks Cole, London.Google Scholar
Rachev, S. T. (1991) Probability Metrics and the Stability of Stochastic Models. Wiley, New York.Google Scholar
Simonot, F. (1995) Sur l'approximation de la distribution stationnaire d'une chaîne de Markov stochastiquement monotone. Stoch. Proc. Appl. 56, 133–149.Google Scholar
Simonot, F. and Song, Y. Q. (1996) Characterization of convergence rates for the approximation of the stationary distribution of infinite monotone stochastic matrices. J. Appl. Prob. 33, 974–985.CrossRefGoogle Scholar
Takács, L. (1962) An Introduction to the Theory of Queues. Oxford University Press, Oxford.Google Scholar
Tijms, H. C. (1986) Stochastic Modelling and Analysis. Wiley, New York.Google Scholar
Willmot, G. E. (1988) A note on the equilibrium M/G/1 queue length. J. Appl. Prob. 25, 228–231.CrossRefGoogle Scholar