Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-22T04:35:37.306Z Has data issue: false hasContentIssue false
  • English
  • Français

Compound Poisson approximations for word patterns under Markovian hypotheses

Part of: Combinatorial probability Markov processes Limit theorems

Published online by Cambridge University Press:  14 July 2016

Mark X. Geske ,
Anant P. Godbole ,
Andrew A. Schaffner ,
Allison M. Skolnick  and
Garrick L. Wallstrom
Mark X. Geske*
Affiliation:
St. Norbert College
Anant P. Godbole*
Affiliation:
Michigan Technological University
Andrew A. Schaffner*
Affiliation:
University of Washington
Allison M. Skolnick*
Affiliation:
Lehigh University
Garrick L. Wallstrom*
Affiliation:
University of Minnesota
*
∗Postal address: CUNA Mutual Insurance Group, Madison, WI 53701, USA.
∗∗Postal address: Department of Mathematical Sciences, Michigan Technological University, Houghton, MI 49931, USA.
∗∗∗Postal address: Department of Statistics, University of Washington, Seattle, WA 98195, USA.
∗∗∗∗Postal address: 88 Stratford Road, East Brunswick, NJ 08816, USA.
∗∗∗∗∗Postal address: School of Statistics, University of Minnesota, Minneapolis, MN 55455, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

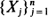Consider a stationary Markov chain with state space consisting of the ξ -letter alphabet set Λ= {a1, a2, ···, aξ }. We study the variables M=M(n, k) and N=N(n, k), defined, respectively, as the number of overlapping and non-overlapping occurrences of a fixed periodic k-letter word, and use the Stein–Chen method to obtain compound Poisson approximations for their distribution.

Keywords

OVERLAPPING AND NON-OVERLAPPING OCCURRENCES OF WORD PATTERNSPOISSON AND COMPOUND POISSON APPROXIMATIONSTEIN–CHEN TECHNIQUECOUPLINGRATES OF CONVERGENCE TO STATIONARITY

MSC classification

Primary: 60F05: Central limit and other weak theorems
Secondary: 60C05: Combinatorial probability 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Type
Research Papers
Information
Journal of Applied Probability , Volume 32 , Issue 4 , December 1995 , pp. 877 - 892
Copyright
Copyright © Applied Probability Trust 1995 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research was supported by U.S. National Science Foundation REU Grants DMS-9100829 and DMS-9200409.

References

Arratia, R., Goldstein, L. and Gordon, L. (1989) Two moments suffice for Poisson approximation: the Chen-Stein method. Ann. Prob. 17, 9–25.Google Scholar
Arratia, R., Goldstein, L. and Gordon, L. (1990) Poisson approximation and the Chen-Stein method. Statist. Sci. 5, 403–424.Google Scholar
Barbour, A., Chen, L. and Loh, W.-L. (1992a) Compound Poisson approximation for nonnegative random variables via Stein's method. Ann. Prob. 20, 1843–1866.Google Scholar
Barbour, A., Holst, L. and Janson, S. (1992b) Poisson Approximation. Oxford University Press.Google Scholar
Böker, F. and Serfozo, R. (1983) Ordered thinnings of point processes and random measures. Stoch. Proc. Appl. 15, 113–132.Google Scholar
Brown, T. (1983) Some Poisson approximations using compensators. Ann. Prob. 11, 726–744.CrossRefGoogle Scholar
Chrysaphinou, O. and Papastavridis, S. (1988) A limit theorem on the number of overlapping occurrences of a pattern in a sequence of independent trials. Prob. Theory Rel. Fields 79, 129–143.CrossRefGoogle Scholar
Chrysaphinou, O. and Papastavridis, S. (1990) The occurrence of sequence patterns in repeated dependent experiments. Theory Prob. Appl. 35, 145–152.Google Scholar
Diaconis, P. and Stroock, D. (1990) Geometric bounds for eigenvalues of Markov chains. Ann. Appl. Prob. 1, 36–61.Google Scholar
Fill, J. (1991) Eigenvalue bounds on convergence to stationarity for nonreversible Markov chains, with an application to the exclusion process. Ann. Appl. Prob. 1, 62–87.Google Scholar
Gani, J. (1982) On the probability generating function of the sum of Markov-Bernoulli random variables. J. Appl. Prob. 19A, 321–326.Google Scholar
Godbole, A. (1991) Poisson approximations for runs and patterns of rare events. Adv. Appl. Prob. 23, 851–865.Google Scholar
Godbole, A. and Schaffner, A. (1993) Improved Poisson approximations for word patterns. Adv. Appl. Prob. 25, 334–347.CrossRefGoogle Scholar
Isham, I. (1980) Dependent thinning of point processes. J. Appl. Prob. 17, 987–995.Google Scholar
Roos, M. (1994) Stein's method for compound Poisson approximation: the local approach. Ann. Appl. Prob. 4, 1177–1187.Google Scholar
Serfling, R. (1975) A general Poisson approximation theorem. Ann. Prob. 3, 726–731.Google Scholar
Serfozo, R. (1986) Compound Poisson approximations for sums of random variables. Ann. Prob. 14, 1391–1398.Google Scholar
Wang, Y. (1981) On the limit of the Markov-binomial distribution. J. Appl. Prob. 18, 937–942.Google Scholar